
Assignment 10: Parametric Equations
By:
Jonathan Sabo
Investigate each of the following for:
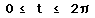 .
.
Descirbe each when a=b, a < b, and a > b.
First we will look at these parametric equations.
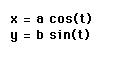
In the first graph we will look at when a = b. In this problem we will set both a and b equal to 1. Using Graphing calculator 3.5 we will graph the given parametric equation.
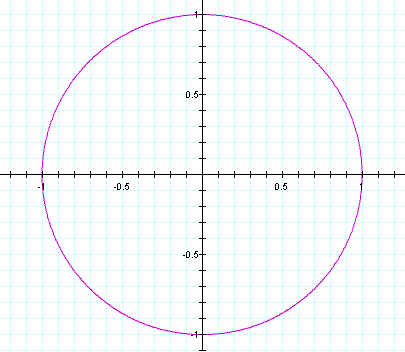
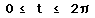 .
.Descirbe each when a=b, a < b, and a > b.
First we will look at these parametric equations.
In the first graph we will look at when a = b. In this problem we will set both a and b equal to 1. Using Graphing calculator 3.5 we will graph the given parametric equation.
Observe, when we have a = b the graph will create a circle.
For the second graph we will look at when a < b. In this problem we will set a equal to 1 and b equal to 3.
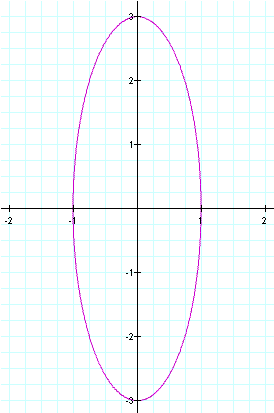
For the third graph we will look at when a > b. In this problem we will set a equal to 3 and b equal to 1.
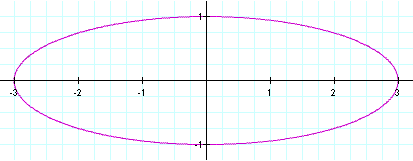
For the second graph we will look at when a < b. In this problem we will set a equal to 1 and b equal to 3.
Observe,
our graph is no longer a circle. It has been stretched
vertically. We can see that our x intercepts are exactly the same
they were at (-1,0) and (1,0) in the previous graph and they are in the
same place now. Our y-intercepts however have been changed, they are now at (0,3) and (0,-3).
For the third graph we will look at when a > b. In this problem we will set a equal to 3 and b equal to 1.
Observe
that this also creates a graph that is not a circle. This graph
has been stretched horizontally. We can see that our y-intercepts
are exactly the same they were at (0,-1) and (0,1) in the original
graph and they are in the same place now. Our x-intercepts
however have been changed, they are now at (-3,0) and (3,0).
Now we will look at the parametric equations:
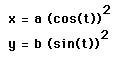
In the first graph we will look at when a = b. In this problem we will set both a and b equal to 1. Using Graphing calculator 3.5 we will graph the given parametric equation.
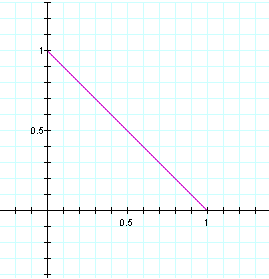
Now we will look at the parametric equations:
In the first graph we will look at when a = b. In this problem we will set both a and b equal to 1. Using Graphing calculator 3.5 we will graph the given parametric equation.
Similar to our first parametric equation we set both a and b equal to 1. We have a x-intercept at (1,0) and a
y-intercept at (0-1). The graph results in a straight line that
is connecting these 2 intercepts. We do not have any negative
intercepts because the cos and sin equations are both being
squared.
For the second graph we will look at when a < b. In this problem we will set a equal to 1 and b equal to 3.
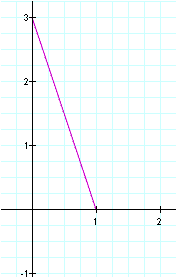
Observe, our graph is now a longer line. It has been stretched
vertically. We can see that our x intercept is exactly the same it
was at (1,0) in the previous graph and it is in the same
place now. Our y-intercept however has been changed, it is now at (0,3).
For the third graph we will look at when a > b. In this problem we will set a equal to 3 and b equal to 1.
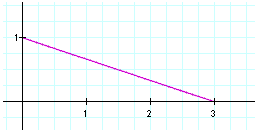
For the second graph we will look at when a < b. In this problem we will set a equal to 1 and b equal to 3.
For the third graph we will look at when a > b. In this problem we will set a equal to 3 and b equal to 1.
Observe that this also creates a graph that is a longer line. This
graph has been stretched horizontally. We can see that our
y-intercept is exactly the same as it was at (0,1) in the
original graph and it is in the same place now. Our x-intercept
however has been changed, it is now at (3,0)
Now we will look at the parametric equations:
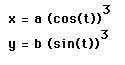
In the first graph we will look at when a = b. In this problem we will set both a and b equal to 1. Using Graphing calculator 3.5 we will graph the given parametric equation.
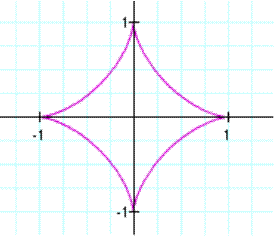
Now we will look at the parametric equations:
In the first graph we will look at when a = b. In this problem we will set both a and b equal to 1. Using Graphing calculator 3.5 we will graph the given parametric equation.
In
this graph we have again have both positive and negative values for x
and y. Now we have x-intercepts at (-1,0) and (1,0) and
y-intercepts at (0,-1) and (0,1). After these observations we can
see that when we have an odd exponent we have graph that has both
negative and positive values for x and y. When we have an even
exponent we would only have either positive exponents or negative
exponents.
For the second graph we will look at when a < b. In this problem we will set a equal to 1 and b equal to 3.
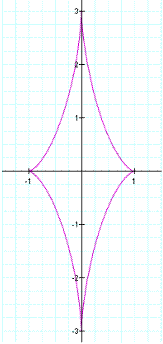
For the second graph we will look at when a < b. In this problem we will set a equal to 1 and b equal to 3.
Observe, our graph has been stretched
vertically. We can see that our x intercepts are exactly the same they were at
(-1,0) and (1,0) in the previous graph and they are in the same place
now. Our y-intercepts however have been changed, they are now at (0,3) and (0,-3).
For the third graph we will look at when a > b. In this problem we will set a equal to 3 and b equal to 1.
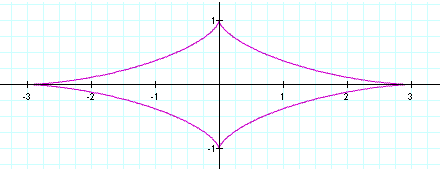
For the third graph we will look at when a > b. In this problem we will set a equal to 3 and b equal to 1.
Observe that this creates a graph that has been stretched horizontally. We can see that our
y-intercepts are exactly the same they were at (0,-1) and (0,1) in the
original graph and they are in the same place now. Our x-intercepts
however have been changed, they are now at (-3,0) and (3,0).
Return to Home Page
Return to Home Page