Examine the graph of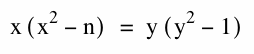 
, where n = 4, 5, 3, 2, 1.1, 1, and 0.9?
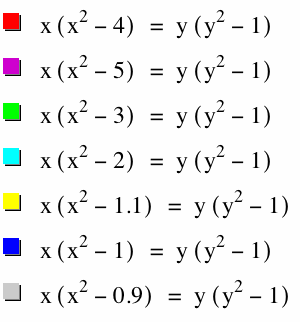
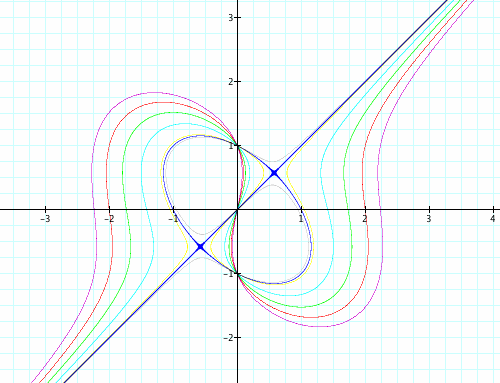
Some observations:
1) Like some cubic graphs, this graph changes direction twice (i.e. the graph increases, decreases, then increases again)
2) They appear to be asymptotic to the line y = x.
3) The y-intercepts are -1, 0, and 1 for all graphs. This is due to the right side of the equation remaining the same at 
.
4) The x-intercepts are 0, -
, and .
5) There is a special case where n = 1. The graph is formed by an oval and a line. If the equation 
is manipulated, you can find the equations of these two graphs.
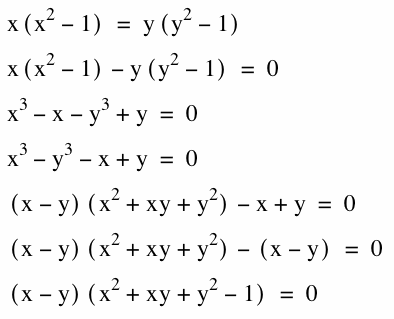
So, the equation of the line is 
and the equation of the oval is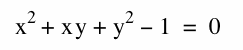 
. To check, I will graph these two equations and compare it to the graph of
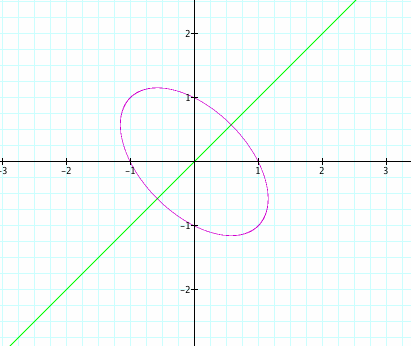
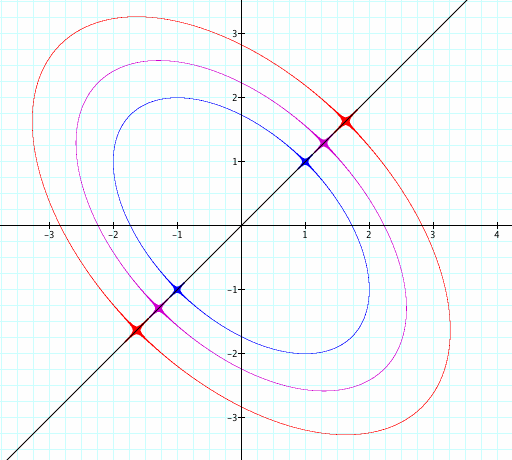
From this, I can assume that if the equation has the same constant on both sides, then the equation will factor. Thus, giving us two graphs, a line and an oval. See below for more examples:
Below is the proof that the same constant on both sides yields a factorable equation.
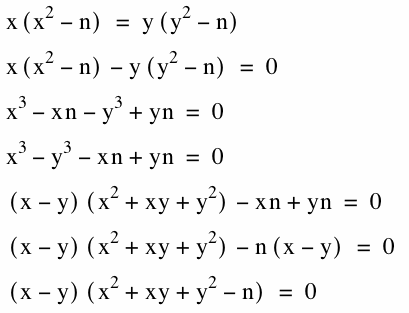
From this, I know that the graph of 
yields the graph of the line y = x and the oval
, which has x and y-intercepts equal to -and.
Now, let's consider the case that n<0. Let's try -4, -8, -5, -1, and -0.9.
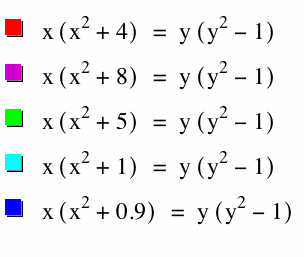
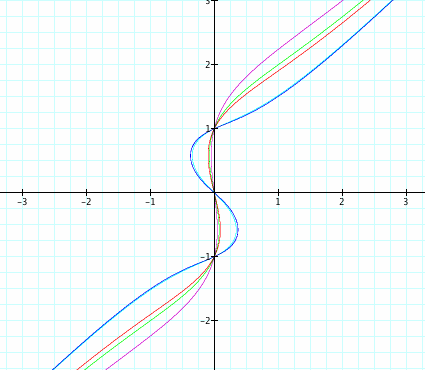
Some observations:
1) Although all cubic graphs change concavity, some of them do not change direction at all (i.e. the graph is always increasing or always decreasing). This graph is similar to this type of cubic.
2) As n increases, the graph seems to be getting more curvy.
3) The y-intercepts are -1, 0, and 1 for all graphs. This is due to the right side of the equation remaining the same at ,
4) There are no x-intercepts. If we attempt to take the square root of n (like in the previous examples), we will get imaginary numbers, which explains why there are no x-intercepts.