by: Doris Santarone
Assignment #10: Parametric Equations
A parametric curve in the plane is a pair of functions x = f(t) and y = g(t) where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t and your work with parametric equations should pay close attention the range of t . In many applications, we think of x and y "varying with time t " or the angle of rotation that some line makes from an initial location.
For this assignment, I will focus on using parametric equations to generate linear graphs.
TRIAL #1
First, I will graph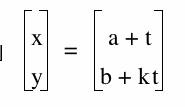 
where a = 1, b = 2, and t = -1...1.
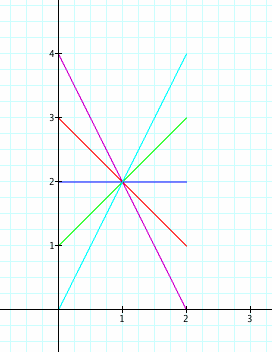
Below are several graphs, for different values of k.
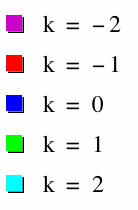
Observations:
1) All of the graphs are line segments with domain (0, 2).
2) All of the graphs share a common point (1, 2).
3) The graphs have different slopes, where the slope of each is k.
TRIAL #2
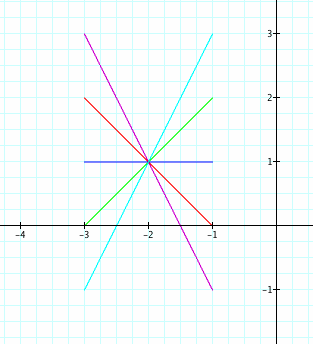
Now, I want to try the same thing, but I will now use a = -2, b = 1, t = -1...1, and vary the values of k.
Observations
1) All of the graphs are line segments with domain (-3, -1).
2) All of the graphs share a common point (-2, 1).
3) The graphs have different slopes, where the slope of each is k.
From the two sets of observations above,
1) It is clear that k tells us the slope of the line segment.
2) It also seems that the common point is (a, b). If we start with the first equation x = a + t and solve for t. So, t = x - a. Then, I will substitute this into the second equation, y = b + kt --> y = b + k(x-a). Using what I know about translations, I can see that this is the equation of the line y = kx, translated b units vertically and a units horizontally.
3) I suspect that the domain is found by a - t, a + t. (We used t = -1...1, so our domain was found by a - 1, a + 1.) To verify this, I will change the t values to -2...2 for TRIAL #1 and TRIAL #2.
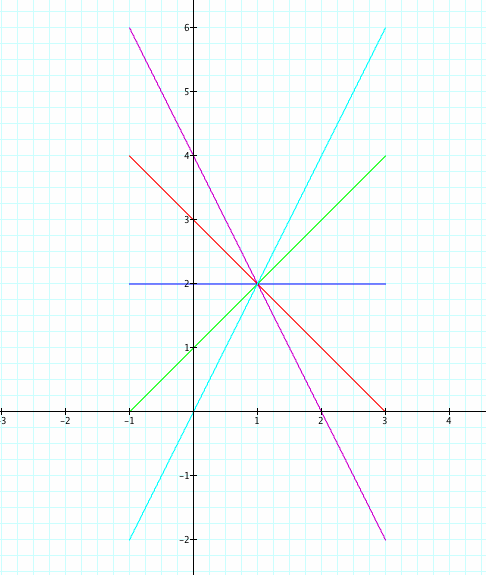
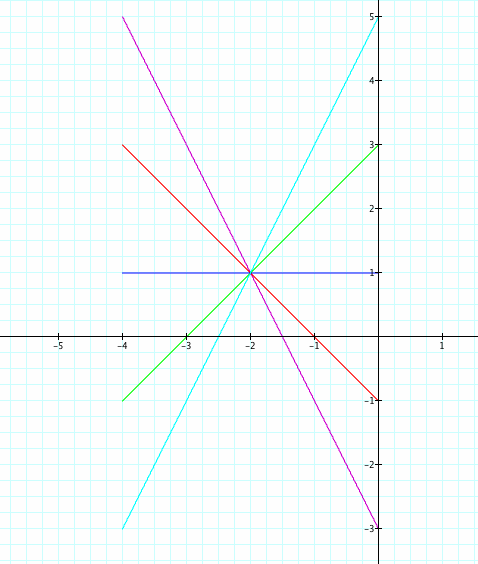
Yes! The only change in the graphs is the domain. For TRIAL #1, the domain is now (-1, 3), and for TRIAL #2, the domain is now (-4, 0). This verified that the domain was found by (a - t, a + t).
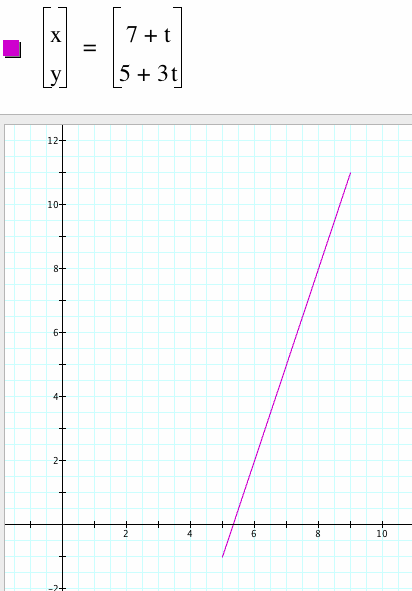
Graph the line segment through (7, 5) with slope = 3
From the findings above, I know that:
1) k = slope, so k = 3,
2) the point (a,b) is on the graph, so a = 7, b = 5.
3) I will set the t values from -2...2, so the domain will be (7-2, 7+2), or (5,9).
