
by: Doris Santarone
Assignment #6: Construct a Triangle, given its Medians
Our goal is to construct a triangle given the three medians. Below are the three medians that we are given, j, k, and m.
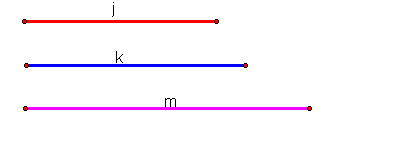
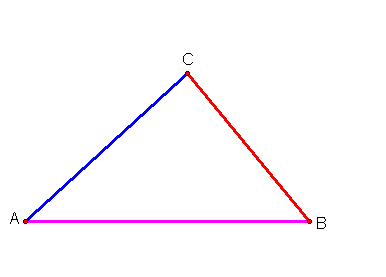
First, we will construct a triangle formed by the medians. We will call this triangle ABC.
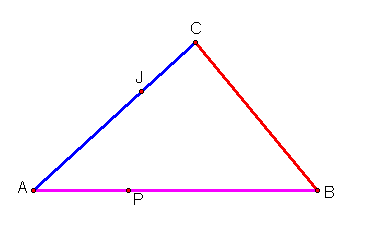
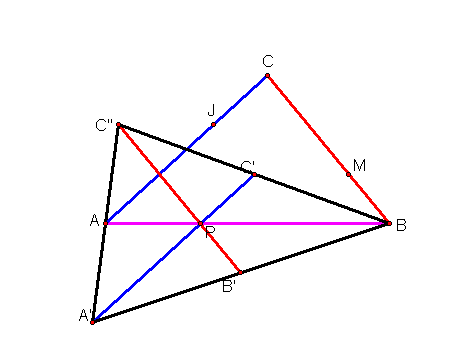
Our goal is to have these three medians concur at one point within the unknown triangle. We also know that they intersect at a point that is 1/3 the distance of the median. So, next I will trisect segment AB, and call this point P. And trisect segment AC, and call it J.
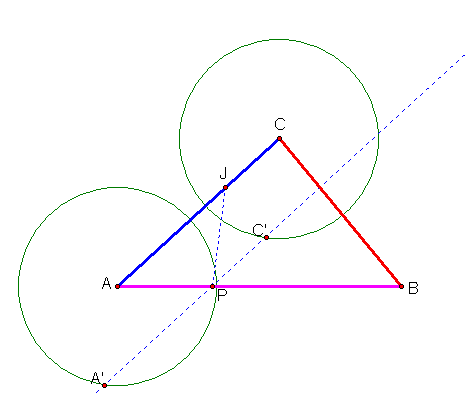
Next, I am going to construct a line through point P parallel to segment AC. Then I will construct a circle with center C, and radius JP. The intersection of the circle and the parallel line will be C’. I will also construct a circle with center A, and radius JP. The intersection of the circle and the parallel line will be A’.
Now, construct the segment A’C’.
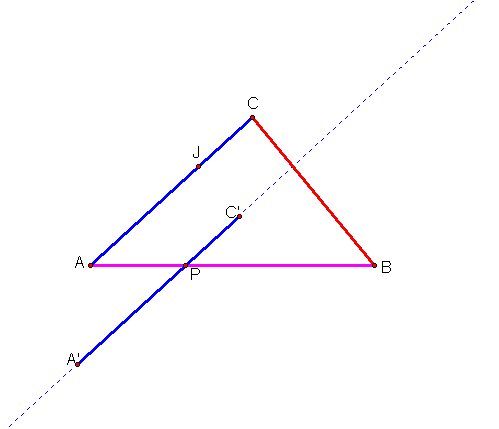
We now have two of the medians (A’C’ and AB) intersecting at 1/3 the length of the medians. We will use the same process in order to get median BC to intersect at the point P at 1/3 its length. First, I need to trisect segment BC. I will call this point M.
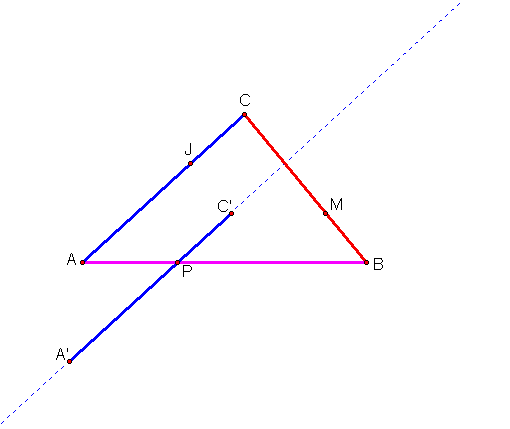
Next, I will construct a line through point P parallel to BC. Then I will construct a circle with center C, and radius MP. The intersection of the circle and the parallel line will be C’. I will also construct a circle with center A, and radius JP. The intersection of the circle and the parallel line will be A’.
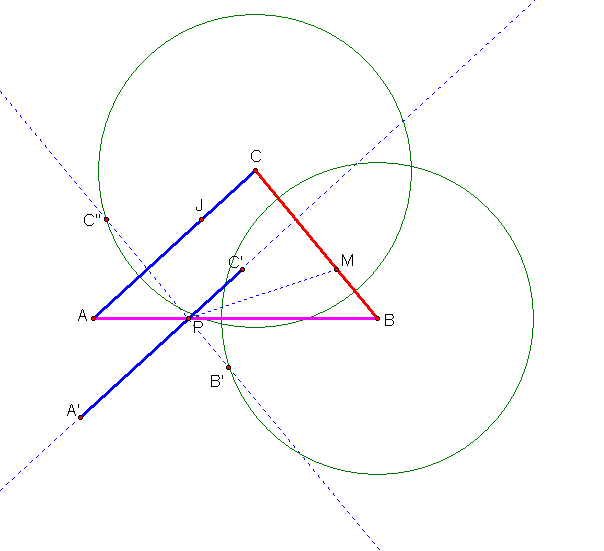
Now construct the segment B’C’’.
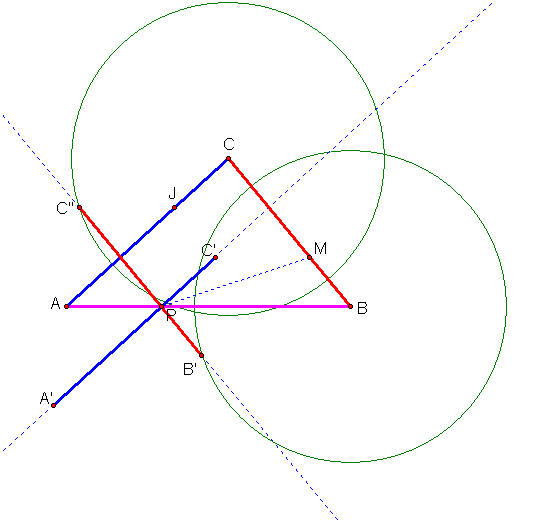
We now have all three medians intersecting at 1/3 their length.

Finally, I will construct the triangle with these three segments as its medians.
Now that we have our triangle, we might want to check to make sure that segments j, k, and m do actually intersect the triangle’s midpoints. We can also check our construction by changing the size of the medians and seeing that the construction remains consistent. Click here to explore this in GSP (with the script).