
by: Doris Santarone
Assignment #7: Tangent Circles
For this assignment, we want to investigate tangent circles. Given 2 circles and a points on one of the circles, construct a circle tangent to the two circles with one point of tangency being the designated point.
Investigation #1: Disjoint Circles
Part 1:
Let's start with our 2 disjoint circles, AB and CD, and a point on circle AB, named E. Point E will be the point of tangency on circle AB.
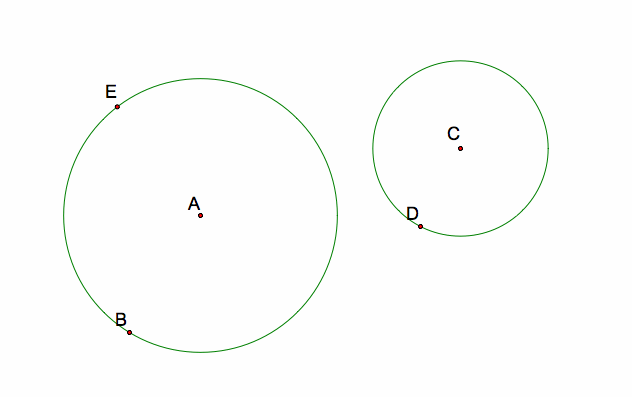
Next, I will construct a line through points A and E. Then, construct a circle with center E and radius CD. This circle intersects line AE at a point, which I will call F. (NOTE: Circle EF intersects line AE in two locations. For now, I will choose the point that lies outiside circle AB; then, I will come back in Part 2 and try the one that lies inside of circle AB.)
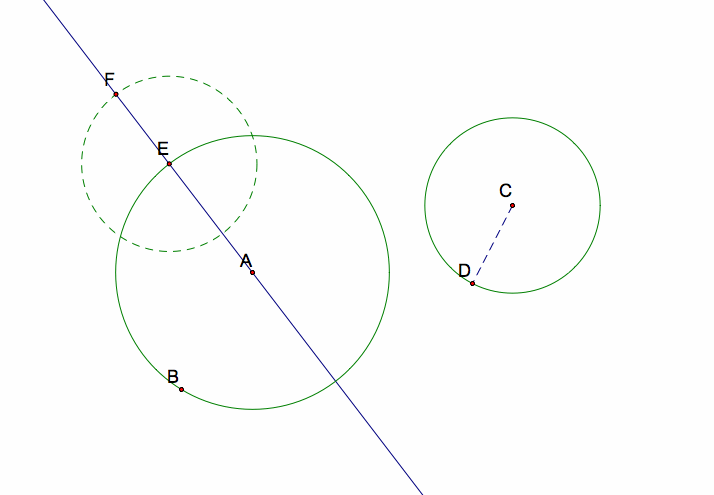
Now, I will construct segment CF. Then, construct segment CF's perpendicular bisector (through midpoint G). This perpendicular bisector will intersect line AE at a point I will call H.
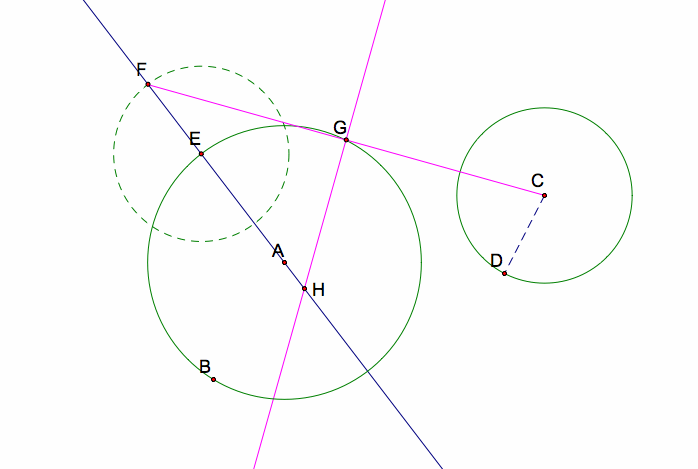
From what we know about perpendicular bisectors, segments FH and CH are congruent. We also know, by construction, that segments EF and CJ are congruent (radii of congruent circles). Thus, FH - EF = CH - CJ, or HE = HJ.
From this, we can construct a circle at center H, with radius HE (or HD). This circle will be tangent to circle AB at point E and tangent to circle CD at a new point (J).
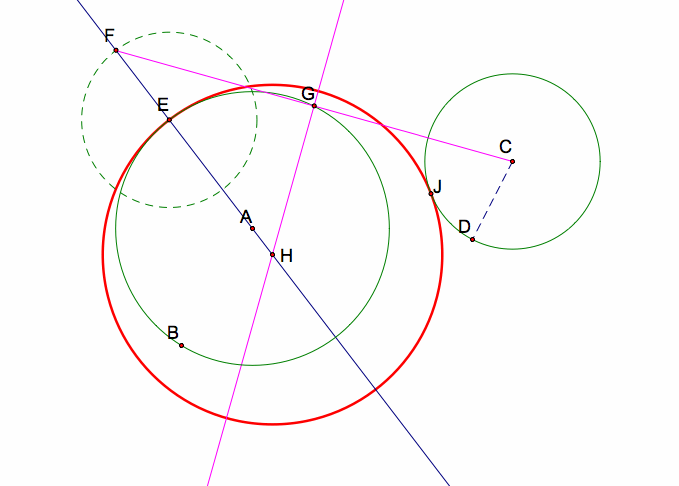
After hiding all of the construction pieces, here is the resulted tangent circle:
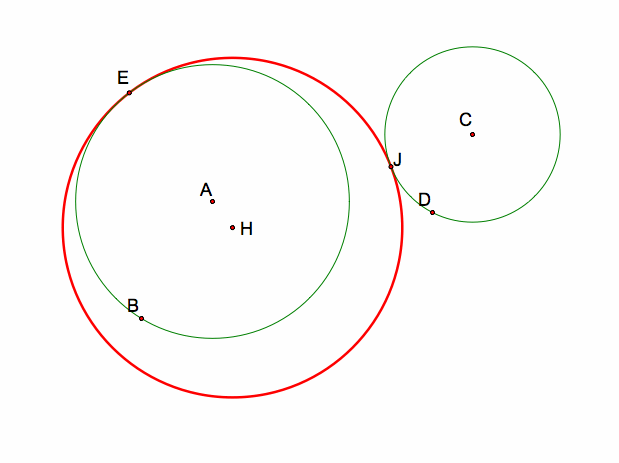
For the GSP Sketch (and script), click here.
Part 2:
As I was doing this construction, I noticed that circle EF intersected line AE in two locations (one outside circle AB and one inside circle AB). I wanted to go back and do this construction with the point of intersection inside circle AB.
I started, again, with two circles AB and CD and a point on circle AB, called E. Then, I constructed a line through points A and E. Next, I constructed a circle at center E with radius CD.
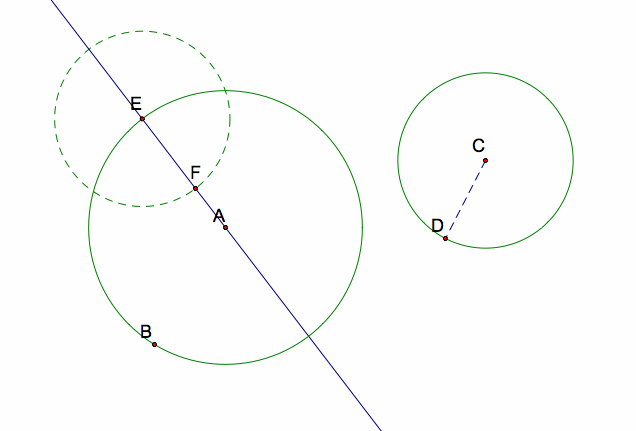
Next, I constructed segment FC and then constructed its perpendicular bisector (through midpoint G). The perpendicular bisector intersects line AE at point H.
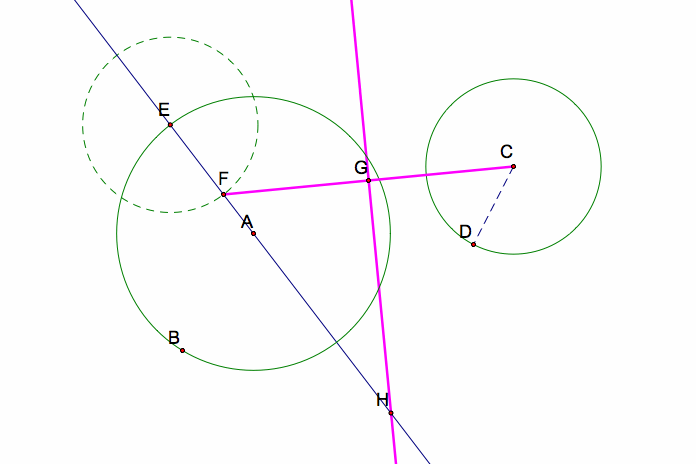
From what we know about perpendicular bisectors, segments FH and CH are congruent. We also know, by construction, that segments EF and CJ are congruent (radii of congruent circles). Thus, FH + EF = CH + CJ, or HE = HJ.
Finally, we will construct a circle at center H, with radius HE (or HJ). This circle is tangent to circle AB at point E and tangent to circle CD at point J.
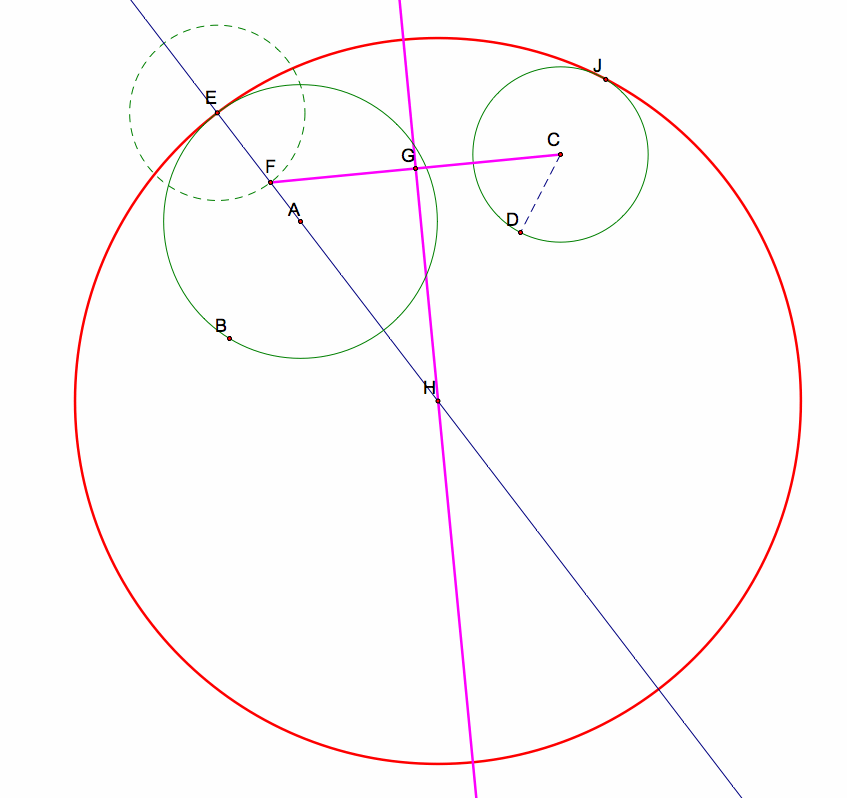
After cleaning up the construction pieces, here is the tangent circle:
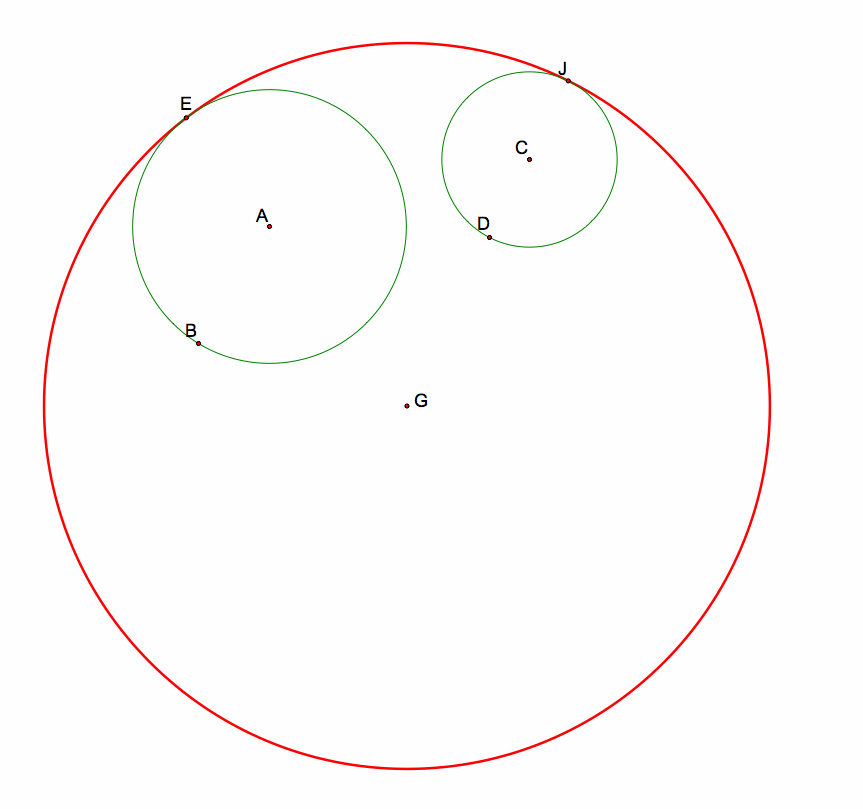
To see the GSP Sketch (and script), click here.
Part 3: Comparing the constructions from Part A and Part B
In Part A (as seen below), the tangent circle (red circle) is tangent to circle AB at point E and it CONTAINS circle AB. It is also tangent to circle CD at point J and it DOES NOT CONTAIN circle CD.

In Part B (as seen below), the tangent circle (red circle) is tangent to circle AB at point E and tangent to circle CD at point J. This time, in contrast to last time, the tangent circle CONTAINS both circles AB and CD.

Investigation #2: Intersecting Circles
Part 1:
This construction is the same as Investigation #1: Part 1. This time, I started with circles AB and CD intersecting. Here is the resulting tangent circle:
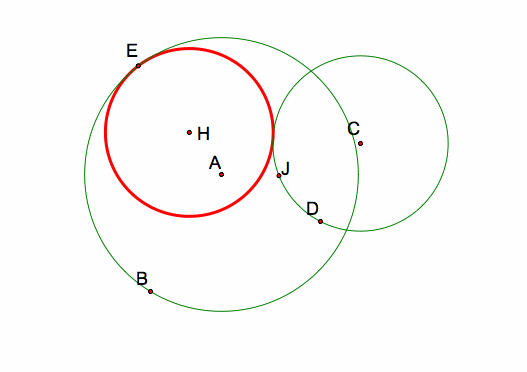
The tangent circle is CONTAINED IN circle AB but NOT CONTAINED IN circle CD. This outcome is similar to (but not the same as) that of Investigation #1: Part 1. One circle is contained and one is not contained.
Part 2:
The construction is the same as Investigation #2: Part 2. Again, circles AB and CD are intersecting this time.
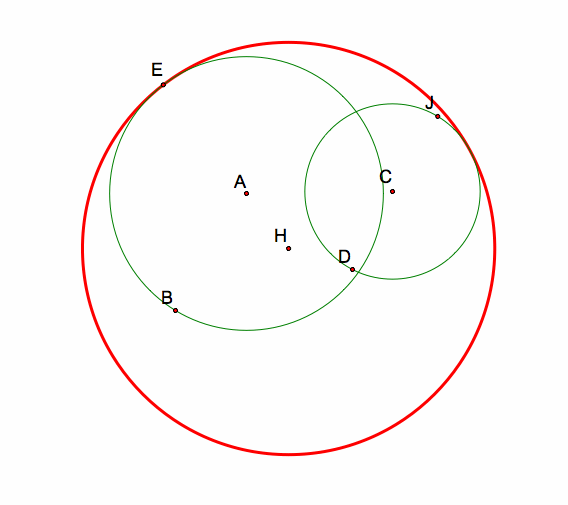
This time, the tangent circle CONTAINS both circles AB and CD. This outcome is the same as in Investigation #1: Part 2.
Investigation #3: One Circle Lies Inside the Other
Part 1:
This construction is done using the same steps as in Investigation #1: Part A. This time, I started with circle CD lying inside of circle AB.
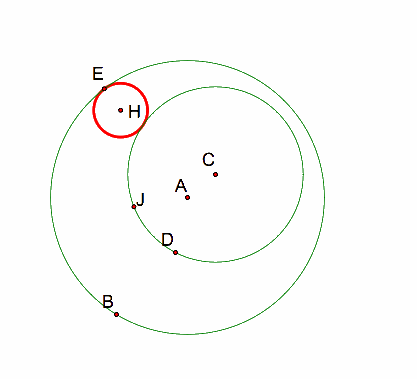
The tangent circle is CONTAINED IN circle AB and NOT CONTAINED IN circle CD. This outcome is similar to the outcome from Investigation #1: Part 1 and Investigation #2: Part 1. Again, one is contained and one is not contained.
Part 2:
This construction is done using the same steps as in Investigation #1: Part B. Again, this time I started with circle CD lying inside circle AB.
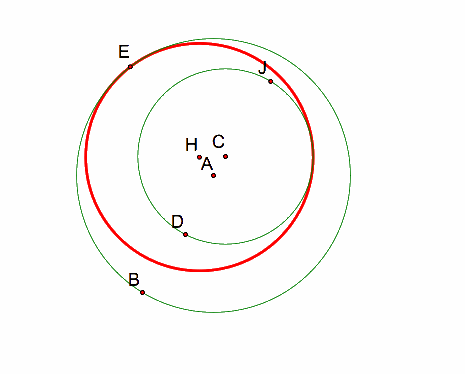
The tangent circle is CONTAINED IN circle AB and it CONTAINS circle CD. This outcome is different than that of Investigation #1: Part 2 and Investigation #2: Part 2. For these, both circles were contained, and this time, only one circle is contained.