
by: Doris Santarone
Assignment #8: Properties of the Orthocenter
Consider triangle ABC, and its orthocenter H.
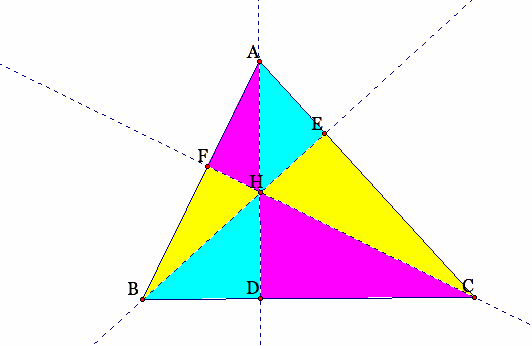
Goal #1: Prove 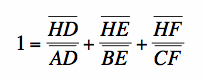
Consider the area of triangle ABC.
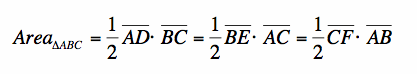
From this, we can find that 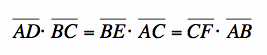 . We will use this later*.
. We will use this later*.
Going back to the area of triangle ABC...we could consider this triangle as a sum of three smaller triangles, triangle BHC, triangle AHB, and triangle AHC:
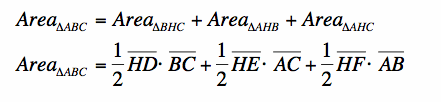
Now, I will use the two equations 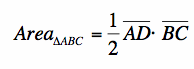 and
and 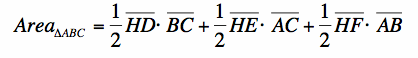 and substitute, giving me:
and substitute, giving me:
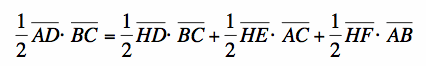
With some manipulation, I get:
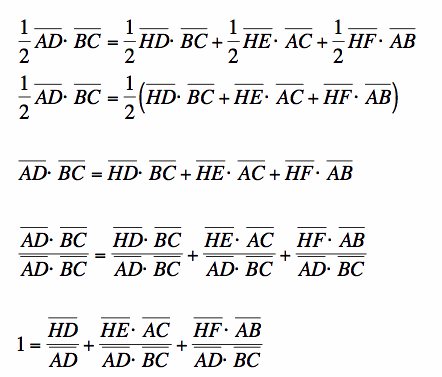
From the equation* that I mentioned before, 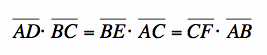 , we can substitute into the denominators of the 2nd and 3rd ratios, and we get:
, we can substitute into the denominators of the 2nd and 3rd ratios, and we get:
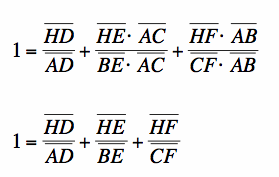
Goal #2: Prove 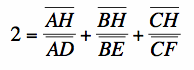
From before, I already know that 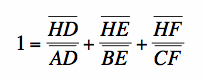 . I also know, using segment addition, that:
. I also know, using segment addition, that:
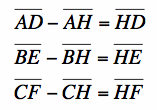
Now, I will substitute:
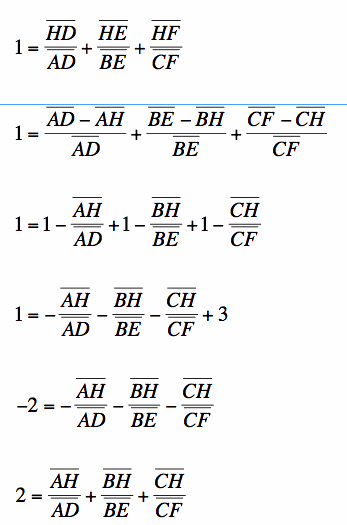
What if the triangle is changed to an obtuse triangle? Consider the image below:
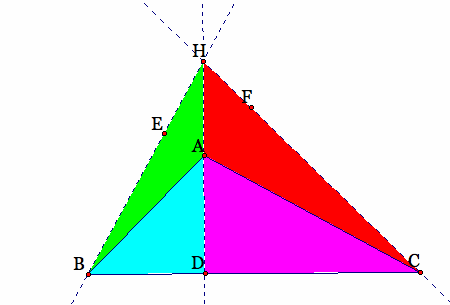
As you can see, ![]() , thus
, thus  .
.
If  and
and 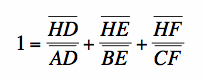 , then
, then 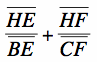 would have to be less than 0, and that is not possible.
would have to be less than 0, and that is not possible.
So, we can conclude that the property 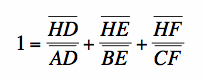 does NOT generalize to obtuse triangles!
does NOT generalize to obtuse triangles!
Similarly, you can see that ![]() , thus
, thus 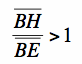 . And
. And ![]() , thus
, thus 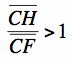 .
.
If 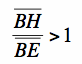 and
and 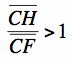 , then
, then 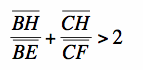 .
.
If 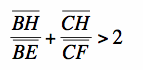 and
and 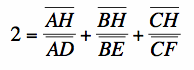 , then
, then ![]() would have to be less than 0, which is impossible.
would have to be less than 0, which is impossible.
So, we can conclude that the property 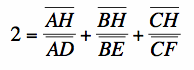 does NOT generalize to obtuse triangles.
does NOT generalize to obtuse triangles.
To see the GSP Sketch, click HERE. Make sure to move the triangle around to see that the properties remain true, except when the triangle is an obtuse triangle.