
by: Doris Santarone
Assignment #9: Pedal Triangles
Construction of a Pedal Triangle
First, I need a triangle ABC and a point P (called the Pedal Point).
Next, I will extend the sides of the triangle to form lines. Then, construct lines through P and perpendicular to each side of triangle ABC. (Line through P perpendicular to AB, line through P perpendicular to BC, and a line through P perpendicular to AC). The points where these perpendiculars intersect the sides (or their extensions) are points R, S, and T. Points R, S, and T form the Pedal Triangle (shown below in pink).
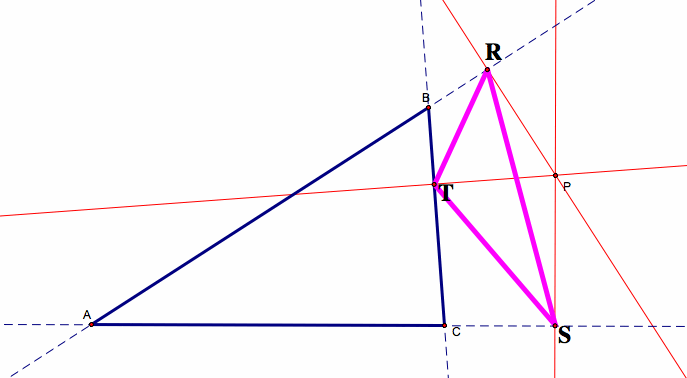
Now, after cleaning it up a little...

Click HERE for the GSP Sketch and script.
What happens if the Pedal Point (P) is one of the triangle centers? Let's see...
1) What happens if the Pedal Point (P) is the incenter?
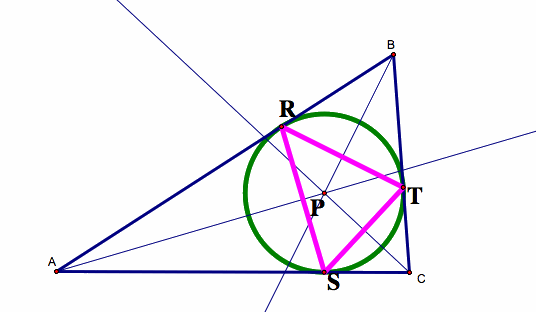
If P is the incenter of triangle ABC, then P is also the circumcenter of the Pedal Triangle (triangle RST).
Click HERE for the GSP Sketch, where P is the incenter.
2) What happens if the Pedal Point (P) is the orthocenter?
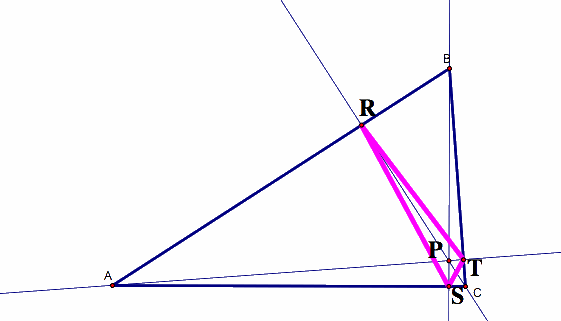
If P is the orthocenter of triangle ABC, then the Pedal Triangle (triangle RST) becomes the Orthic Triangle, which is the triangle formed by the feet of the altitudes.
But, what if the orthocenter is on the outside of triangle ABC?
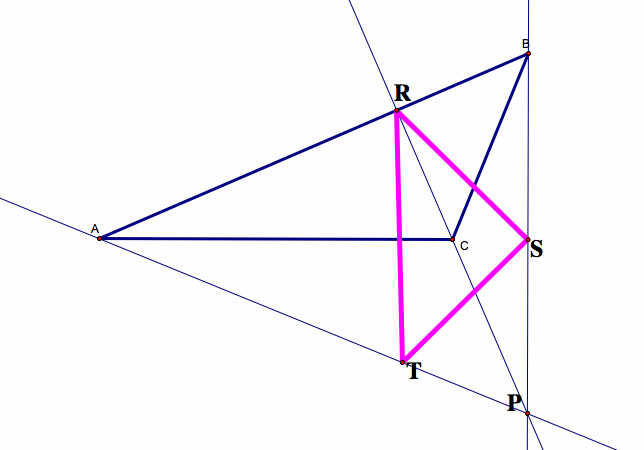
This time, the Pedal Triangle (triangle RST) is the Orthic Triangle of triangle ABP (as opposed to the original triangle, ABC).
Click HERE for the GSP Sketch, where P is the orthocenter.
3) What happens if the Pedal Point (P) is the circumcenter?
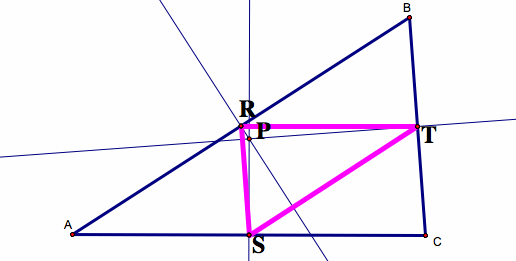
If P is the circumcenter of triangle ABC, then the Pedal Triangle is the Medial Triangle, the triangle formed by the midpoints of each side of the triangle.
But, what if the circumcenter were outside the triangle?
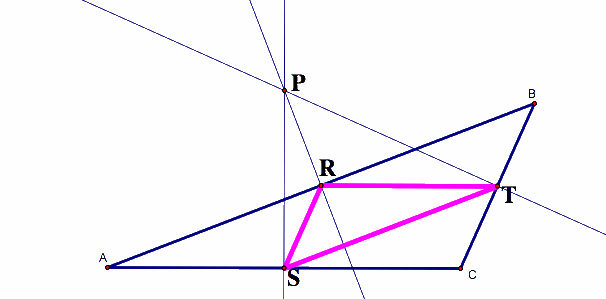
The Pedal Triangle is still the Medial Triangle!!
Click HERE for the GSP Sketch, where P is the circumcenter.
What happens if the Pedal Point (P) is on the triangle? Let's see...
1) What if the Pedal Point (P) is on one of the sides of the triangle?
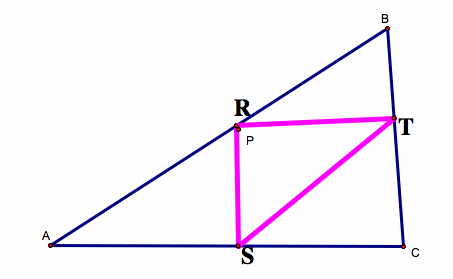
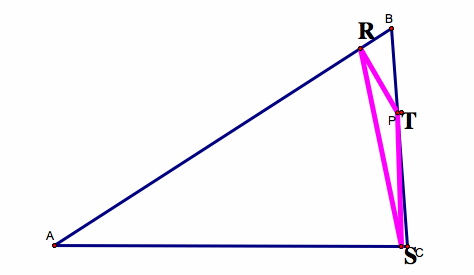
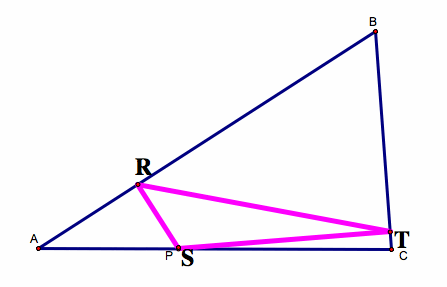
When the Pedal Point (P) is on a side of the triangle, P becomes one of the vertices of the Pedal Triangle.
2) What if the Pedal Point (P) is on one of the vertices of the triangle?
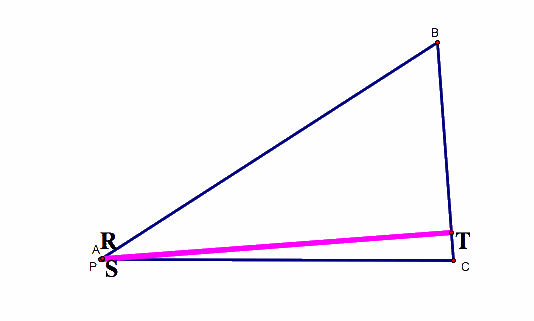
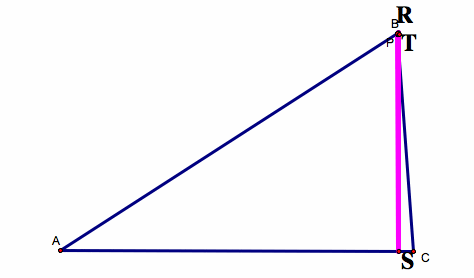
If the Pedal Point (P) lies on a vertex of the triangle, then P coexists with two vertices of the Pedal Triangle. Because there are now only 2 points making up the Pedal "Triangle", the Pedal Triangle is now a segment. This segment is called the Simpson's Line.