
by: Doris Santarone
Modular Arithmetic
Intro to "Clock Arithmetic"
Modular arithmetic is also known as "clock arithmetic". When dealing with modular numbers, it is helpful to think of the face of a clock, like the one here:
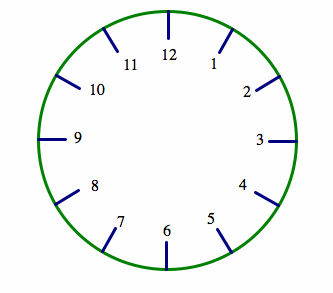
The numbers go from 1 to 12. So, what happens when you get to "13 o'clock"? "13 o'clock" actually becomes 1 o'clock again. So 13 becomes 1, 14 becomes 2, and so on. See the clock below for an illustration.

This can keep going, so when you get to "25 o'clock'', you are actually back round to where 1 o'clock is on the clock face (and also where 13 o'clock was too). 1,13,25,37,… are all thought of as the same thing, as are 2,14,26,38,… and so on.
In other words, 13 divided by 12 is 1R1, which tells us that we went around the clock (containing 12 numbers) one time with an additional one more step... this would land us at the 1 position on the clock. We would write this as 13 ≡ 1 mod 12 (which is read as "13 is congruent to 1 modulo 12"). Let's do another example: 42 divided by 12 is 3R6. This means that we went around the clock 3 times with an additional 6 steps, which would land us at the 6 position on the clock. We would write this as 42 ≡ 6 mod 12.
Additionally, we prefer to put a 0 in the place of the 12 on the clock. This means that 24≡0 mod 12 rather than 24≡12 mod 12.
Other Modular Numbers
You don't have to work only in mod 12. You could work in any modular number. Suppose we want to work in mod 8. Imagine a clock with the numbers 0-7 on it.

What position on the clock would you find "10 o'clock"? Well, we know that 10 divided by 8 is 1R2, or 10≡2 mod 8. On the clock, "10 o'clock" would be found in the same position as "2 o'clock."
Formal Definition
In general, if you are working mod n (where n is any whole number), we write a≡b mod n if a divided by n gives you a remainder of b.