by: Doris Santarone
Essay #3: Half the Area of a Triangle with a Line Parallel to the Base
Problem
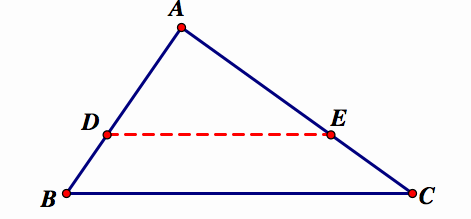
For any triangle, construct a segment parallel to the base of the triangle that divides the triangle into 2 equal areas.
Discussion: Before attempting this problem, I first need to figure out some properties of the triangle, with the assumption that this parallel segment does divide the areas in half. Click here for this discussion.
Construction: Our goal is to construct the segment DE that is parralell to BC and divides the area of triangle ABC in half. From the previous discussion, we now know that the ratio of the sides of triangle ADE to triangle ABC is 
. We can construct this property in order to get the desired segment.
I will focus on the heights. So, first I will construct the height of triangle ABC, AG.
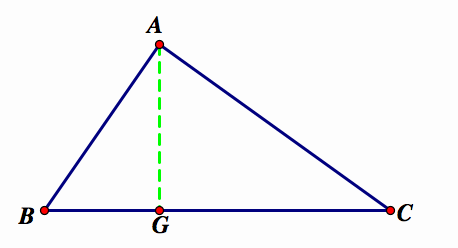
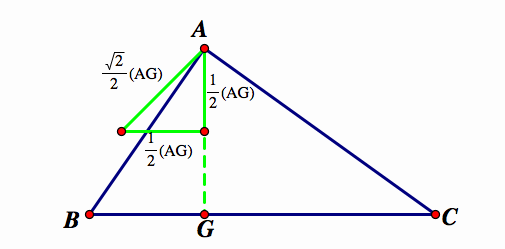
I need to find a point on AG, such that
. I am going to construct a 45-45-90 triangle with side lengths equal to (1/2)AG, (1/2)AG, and 
.
To do this, I will first bisect AG to get one of the legs equal to length (1/2)AG. Then, construct the other leg that is perpendicular to this leg, also of length (1/2)AG. Finally, the hypotenuse of the triangle can be constructed, and it has length .
Finally, will use point A as the center of a circle, with radius equal to . Then, mark the intersection of this circle with AG. This point is named F. Thus .
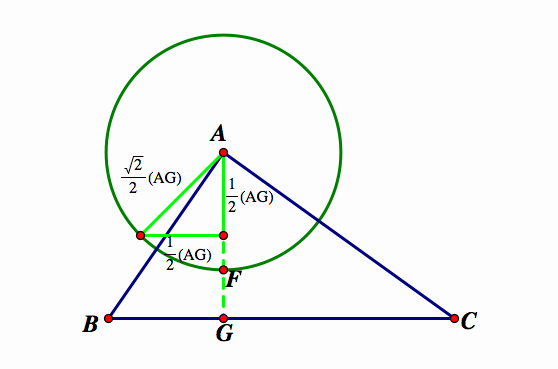
Now, I just need to construct the segment through point F, parallel to BC.
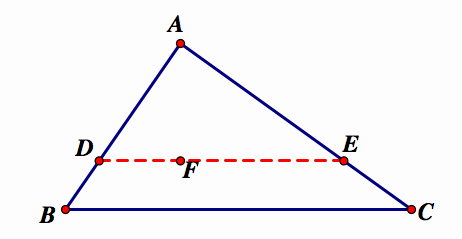
This segment divides the area of triangle ABC in half.
Click here to see the GSP Sketch where you can see move the vertices of triangle ABC and see that the area of triangle ABC is always twice the area of triangle ADE.
Extension
If the parallel segment that divides the triangle into 2 equal areas is drawn for each base, a smaller triangle is formed. What is the ratio of the area of the small triangle to the area of the original triangle?
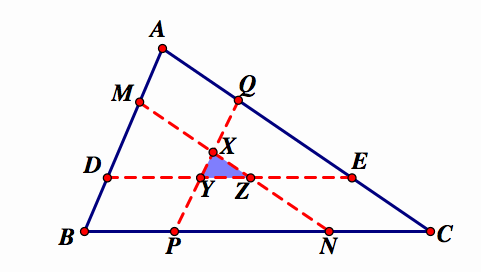
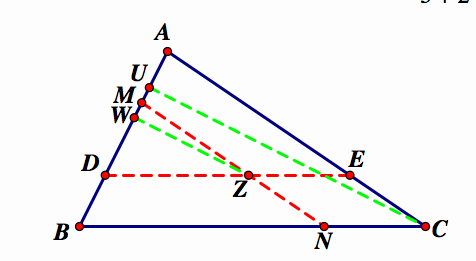
To begin this investigation, I will start with only 2 of the parallel segments constructed:
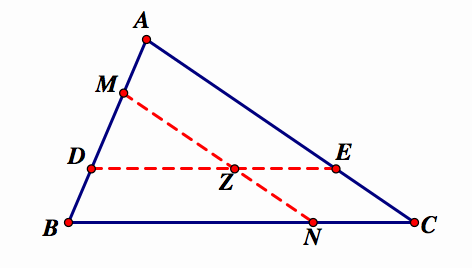
From the previous problem, we know that 
. By the same reasoning, 
.
We also know that segment AB = AD + BM - DM. By substitution,
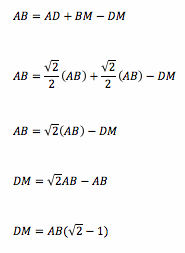
Since the triangles ABC and MZD are similar, then the ratio of all sides and height are the same as above.
Now, let's look at the areas. To do this, I will first need to construct the height of triangle ABC. Remember that we just discovered that the ratios, including the height, of triangle MDZ to ABC is sqrt(2) -1.
The area of triangle ABC is 
. The area of triangle MDZ is:
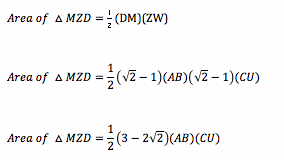
The ratio of the area of triangle ABC to the area of triangle MDZ is:
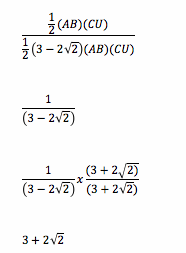
Click here for the GSP Sketch, where you can move the vertices of triangle ABC and see that this relationship is true.
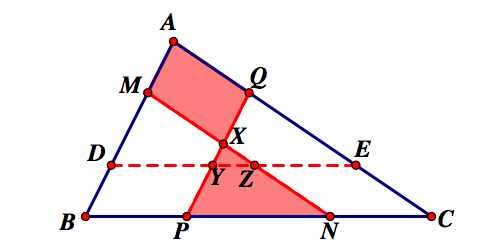
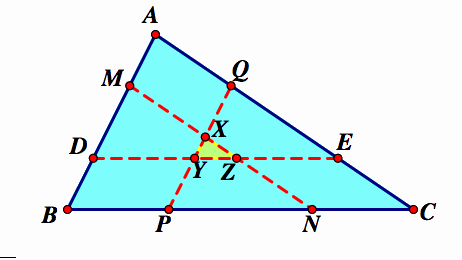
Now, let's draw in the 3rd parallel segment
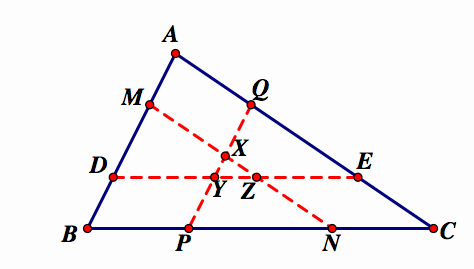
We can assume this same relationship holds true. So, the area of triangle MDZ =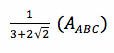 
, the area of triangle QYE = 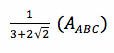, and the area of triangle PXN =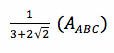
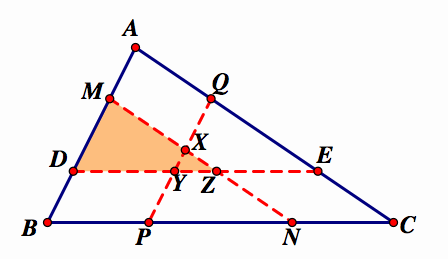
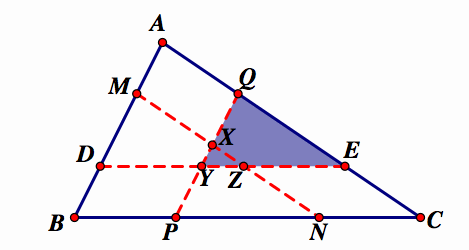
These three small triangles overlap in the middle triangle XYZ. If we subtract the area of XYZ from each triangle above, we would get 3 quadrilaterals with equal area:
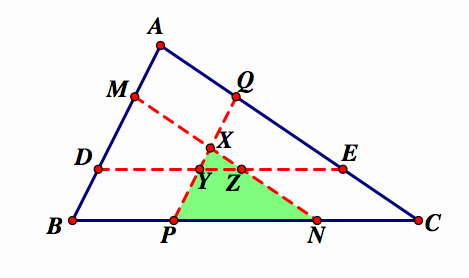
Now, let's take a look at the 3 quadrilaterals formed at each vertex:
Since APBQ is half the area of ABC, and AMNC is also half the area of ABC. Then, quadrilaterals APBQ and AMNC are equal in area. So,
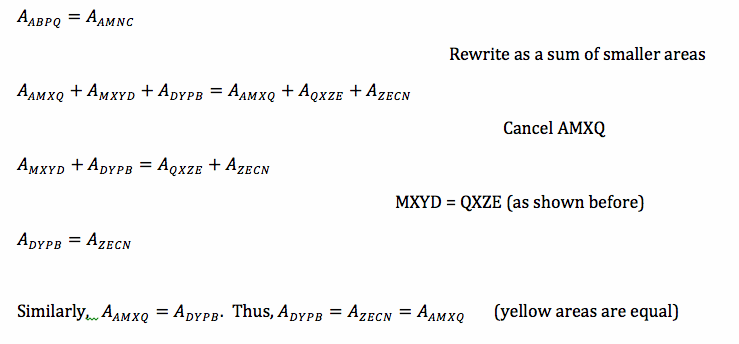
Next, let's look at some other relationships. We know that triangle PQC is half the area of ABC, and also quadrilateral AMNC is half the area of ABC, then the area of PQC and AMNC are equal.
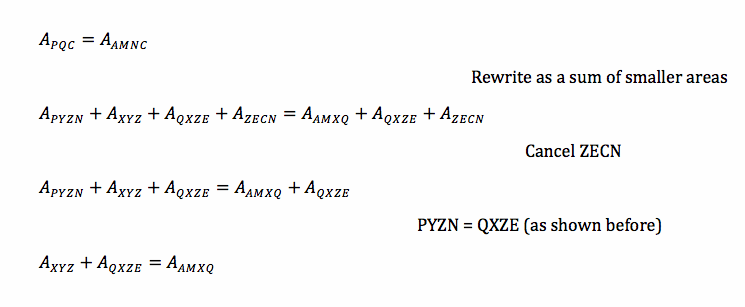
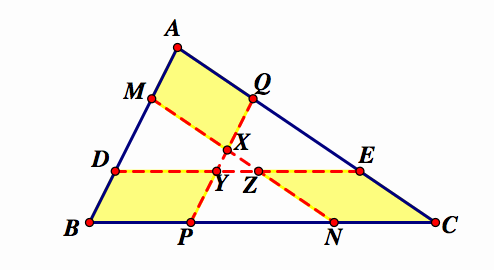
Further,
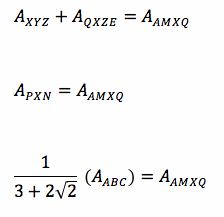
This statement is true for all of the triangles below:
Click here for the GSP Sketch.
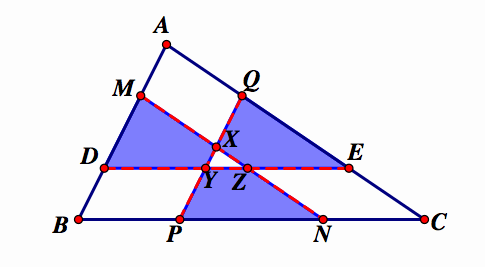
Going back to the blue triangles,
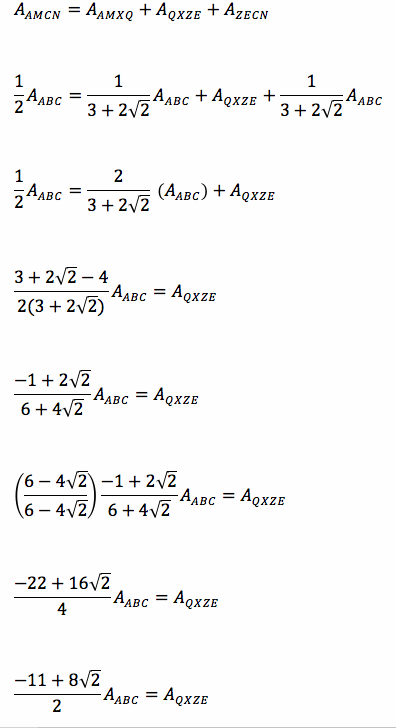
This relationship is true for all of the blue quadrilaterals (pictures above). Click here for the GSP Sketch.
Using all of the information that we've gathered, we want to compare the areas of the small triangle XYZ and the large triangle ABC.
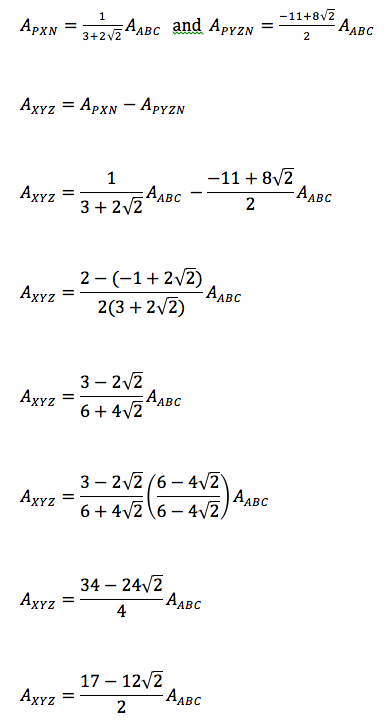
Click here for the GSP Sketch.