by: Doris Santarone
Final Assignment #3: Investigating Trees Using Spreadsheets
This data is from the lumber industry, giving the approximate number of board feet of lumber per tree in a forest of a given age.
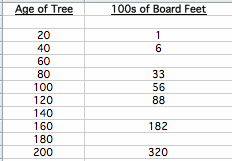
What function will best fit the data? The data is increasing at an increasing rate, forming a concave up curve. It seems that there are several functions that might be ab appropriate fit for the data: exponential, quadratic, or maybe a cubic function. Let's try each of them and see which one fits best (i.e. has the lowest sum of errors squared).
Function #1: Exponential Function
The equation of the exponential function that best fits the data is: 
where B is the number of hundreds of board feet of lumber per tree in a forest of age t.
Below is the graph of the given data (in blue) and the predicted data using the above exponential function (using red).
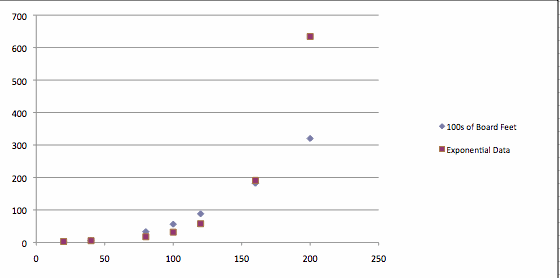
You can see that the given data and the exponential data are very similar at the beginning, but the exponential function increases too quickly as x increases. Below is spreadsheet of the given data and the exponential data, along with the errors.
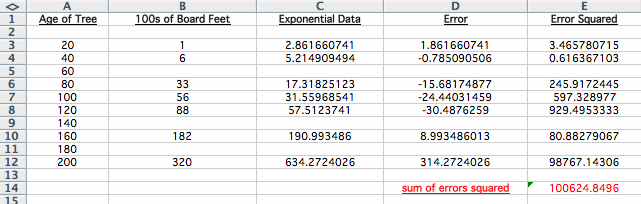
You can see that the sum of the errors squared is 100624.8496.
Click HERE to see the spreadsheet for the exponential function.
Function #2: Quadratic Function
The equation of the quadratic function that best fits the data is: 
where B is the number of hundreds of board feet of lumber per tree in a forest of age t.
Below is the graph of the given data (in blue) and the predicted data using the above quadratic function (using red).
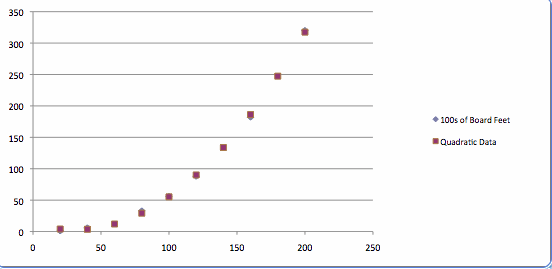
You can see that the given data and the quadratic data are very similar! This seems to be a good fit! Below is spreadsheet of the given data and the quadratic data, along with the errors.
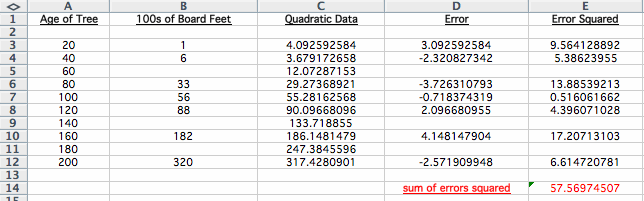
You can see that the sum of the errors squared is 57.56974507.
Click HERE to see the spreadsheet of the quadratic data.
Function #3: Cubic Function
The equation of the cubic function that best fits the data is: 
where B is the number of hundreds of board feet of lumber per tree in a forest of age t.
Below is the graph of the given data (in blue) and the predicted data using the above cubic function (using red).
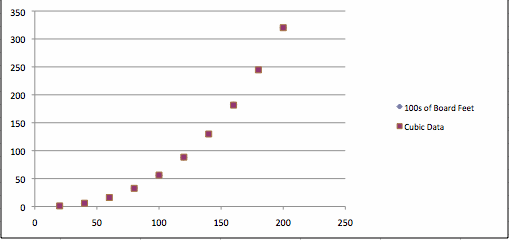
You can see that the given data and the cubic data are very similar! It's hard to tell if this is better than the quadratic, so I'll need to use the spreadsheet to calculate the errors! Below is spreadsheet of the given data and the cubic data, along with the errors.
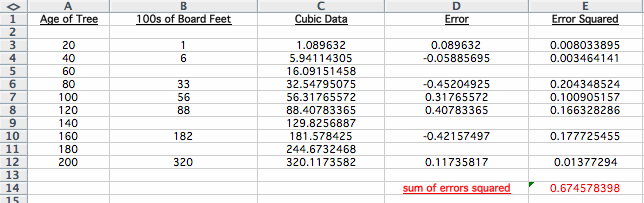
You can see that the sum of the errors squared is 0.674578398. This is definately a better fit than the quadratic!!
Click HERE to see the spreadsheet of the cubic data.
Since the cubic function fit the data best, we can use it to make some predictions. I will interpolate for t =60, 140, and 180 and extrapolate for t = 220, 240, and 260.
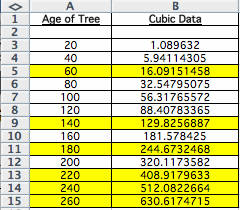
Click HERE to see this spreadsheet. You can also use this spreadsheet to put in any value for t (age of tree) and the spreadsheet will give you the corresponding B (number of hundreds of board feet of lumber per tree in a forest t years old). Enter the desired t into the box below t = 260.