
Exploring
Inscribed Squares in a Half Circle
By: Amanda Sawyer
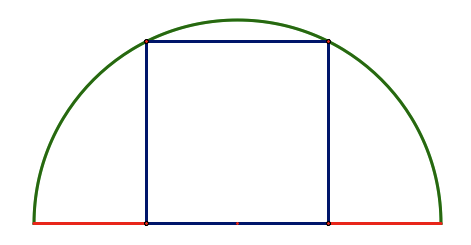
For the following figure, we will determine the ratio of the side length of the inscribed square (s) and the additional distance of the square to the circle (a).
![]()
The picture below shows the labeled areas of our figure.
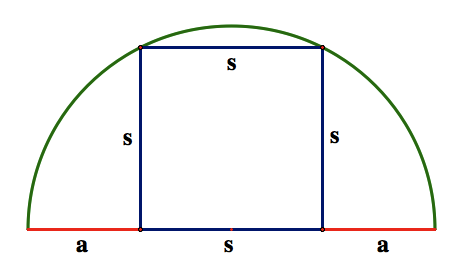
We can already determine certain relationship between s and a by observing the diameter. Notice that we know the diameter of our figure to be:
![]()
This now allows us to determine where the center of our circle occurs.
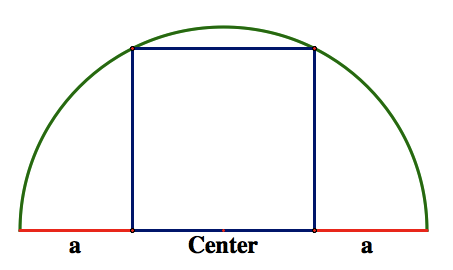
We can notice that it is located directly in the middle of side s. Since we have equal distance of a on both side of the diameter, this means that the center must be the midpoint of s. This gives us the formula for the radius of our circle.
![]()
In the inscribed square, we can find the radius located from the center of our circle to one of its sides as seen below.
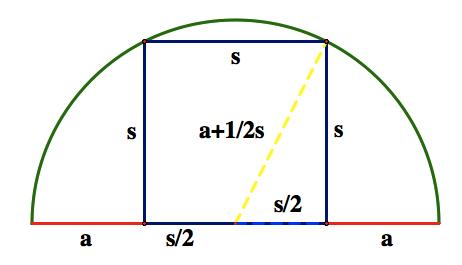
This radius creates a triangle within our shape with a right angle. Therefore, we can use the Pythagorean Theorem to determine a relationship between s and a.
![]()
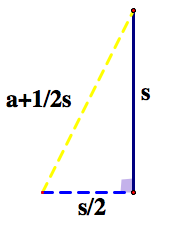
When we simplify the left and right side of the equation, we obtain:
![]()
![]()
By using the quadratic equation, we can solve for s. From this value of s, we can solve for our ratio.
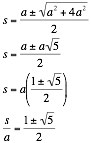
This gives us the two different ratios for the values. However, we know that both s and a will be positive values. Since the ratio of any two positive values must be positive, we only have one value for our ratio:
![]()
We know that this ratio is phi (the golden ratio) which I discussed in detail in Final 3 assignment.