The Study of the Product of Two Quadratic Functions
By: Amanda Sawyer
In the
given problem, we are to explore two quadratic functions with the product of
these quadratic functions creating two different tangent points. The two general quadratic functions
will be named
The
product of these two general quadratic functions will be named
As
we can see, the product produces a fourth degree polynomial. We can study this fourth degree
polynomial and its behavior to the given two functions using Graphing
Calculator. It is known that the
maximum number of turns that a fourth degree polynomial can have is one less
than the degree. Since, the
problem asks for this function to be tangent to both of our given functions at
two points, it will be necessary for the function h(x) to have the three changes in
concavity. It is also known that we must study the relationship between h(x)=0 and f(x)g(x)=0 to
determine what criteria is needed for the intersection of these graphs. To do this, we will set f(x)=g(x)=y,
and study what happens when they create h(x):
Since
, it is easy to see (a+b) = 0, (b+g) = 0, and (f+c) = 1. To show this property, we can calculate
these values using graphing calculator as shown below. It is set such that a=1, d=-1, b=1, g=-1, c=n, and f=1-n. Through this investigation, we can
study what is needed to create the two tangent points. The next three pictures shows how
n effects
the intersection of h(x).
|
The Values of n |
The Graph |
|
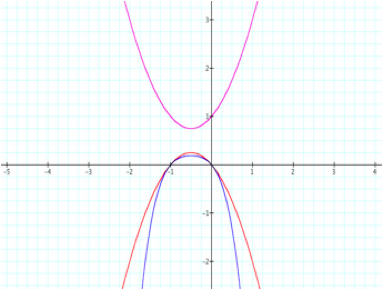
n = 1 |
|
|
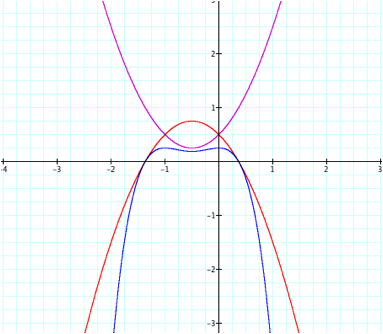
n = 0.5 |
|
|
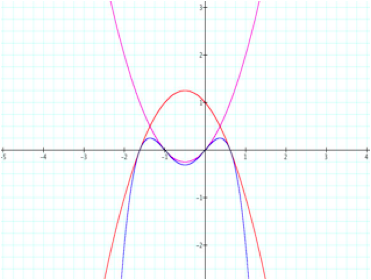
n = 0 |
|
As
we can see, other restrictions are necessary to create this reaction. We also need the two original functions
to intersect at two points. Therefore,
we must set f(x)=g(x). Since we already
know some properties about our variables, we set d=-a, g=-b, f=1-c.
This creates the equation,
This
gives us some restrictions on what our c variable must be to create these
tangent points. Therefore,
for c<.5, the product of these two graphs will
creates two tangent points from the given original functions. From this
investigation, it has been shown that we can use mathematics and technology to
study the effects of given equations.