
Future Value of Simple Interest and Compounded Interest
Investigation
By: Amanda Sawyer
At Charleston Southern University, there is a
course called MATH 105 Introduction to Mathematical Structures.† In this course, we discuss many mathematical
concepts like Set Theory, Basic Algebra, Logic Theory, Data Analysis,
Probability, and Interest.† When we study
interest problems, we always go into A) Future Value of Simple Interest and B)
Future Value of Compound Interest.† Given
some initial amount that we call the principal (P), the number of years you
will use this amount (t), and the interest rate per year (r), we can find its
future value.† In this assignment, we
will investigate different ways of showing the future value of interest using
an excel spreadsheet.
A) Future Value of
Simple Interest
Letís first investigation how
to solve future value of simple interest.† Letís define simple interest. Simple interest
is the amount of money paid on a loan. It is the easiest type of interest to
calculate and understand because its value I = Prt
(Simple Interest = Principal x Interest Rate x Time).† Below you will see example of a simple interest
problem:
If you deposit $800 in an
account paying 6% simple interest for 4 years, determine the amount of interest
earned on the given deposit.
From this, we can find future value of simple interest:
![]()
When A is the future value, we can see that this
amount is just our initial quantity with the addition of simple interest.† An example of a future value of simple
interest problem would be:
If you
deposit $1300 in an account paying 10% simple interest for 2 years, determine
the future value the deposit.
We can have students study this concept using an
Excel Spread Sheet.† In the spreadsheet
the students can have the first input as the principal and second input as the
time in years.† This way they can see how
the interest rate affects the future value.†
They can also play with the values to fully see what happens to the
amount the longer it is used.

You can also look for present value of simple
interest using this kind of excel spread sheet.†
Present value of simple interest is the initial amount of money you will
need to receive a given amount in a given number of years.† For example, a question could ask:†
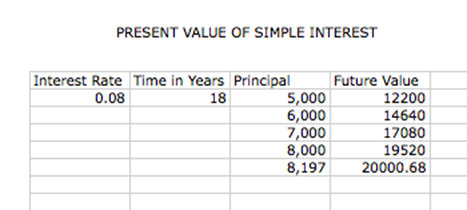
Sam and Diane need to have $20,000 available in 18
years to pay for their daughterís first year of college.† Find the lump sum they must invest now if the investment is paying
8% interest rate per year.
When we place these values into an Excel Spread
sheet the students can use the guess and check method to check their answer.
B)
Future Value of Compound Interest
Next, letís investigate how to find future value
of compound interest. Suppose you open an account that pays a guaranteed
interest rate, compounded annually.† If you
make no further contributions, how much money would you have after t
number of years?† We can calculate this
information as seen from the table below.
|
Year |
Balance |
|
Now |
P |
|
1 |
P+rP |
|
2 |
(P+rP)
+r(P+rP) |
We can see that a pattern is occurring.† This shows us that we can find a formula for
compounded annually interest:
![]()
However if we wanted to find out the future value
of an amount compounded n times a year, we would replace the
1 in the formula with n.† Therefore, our
formula for future value of compound interest is:
![]()
When we study compound interest, we discuss what
will happen if the account is compounded quarterly, semiannually, monthly, and
daily.† Below is a sample problem that
involves finding the future value of compound interest.
If you deposit $5,000 in an account paying 5% interest, how
much money will you receive in 8 years if the account is
a) compounded annually
b) compounded semiannually
c) compounded quarterly
d) compounded monthly
e) compounded daily
Again, we can use a spread sheet to study this behavior.† If we allow the first three columns to be the
principal, interest rate and time in years respectively, we can find out the
future value of these amounts given its nth value as seen below.†
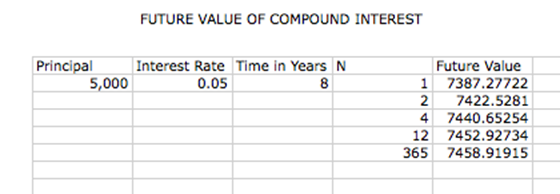
From this spread sheet it shows how each amount is increased by
the nth
value.† Most students assume that the
amount will increase drastically from compounded annually to compounded daily,
but through the use of this spead sheet we are able to see that the difference
is not very large.†
We have investaged two ways of solving interest problems using
Excel Spead Sheets.† Through the use of
these repeating values we can investigae many interseting qualities of
interest, and the ones that I have shown are just the beginning.