
The Construction of Incenters and Circumcenters
By:
Amanda Sawyer
In this
assignment, we will discuss some of the properties of a triangle and their
respected centers. When we study
triangles in any geometry course, we must discuss how a circle can be inscribed
or circumscribed around its shape.
This concept is easy to construct once we have tools that are
accurate. Otherwise, the students
created circles will never demonstrate the properties discussed in class. To
make sure that our points are created correctly we will use Geometer’s Sketch
Pad. In this discussion, I will
discuss how to create a circumcenter and an incenter for any triangle.
When studying
these centers, we first discuss the creation of perpendicular bisectors and
angle bisectors because they are the building blocks for these two centers.
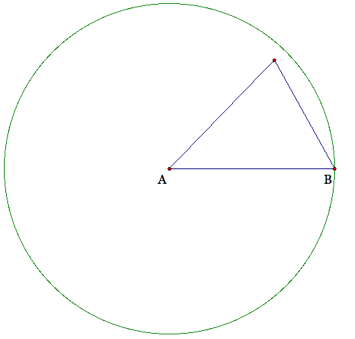
When creating a circumcenter, we find the intersection of the perpendicular
bisectors of each of the three sides of a triangle. This circumcenter is the center of the circle that
circumscribes the shape.
Therefore, we can find a circle with the circumcenter that has a radius
length equal to the distance of all three angle vertices. When creating an incenter, we find the
intersection of the angle bisectors of each of the three angles of a triangle. This point is the center of the circle
that can be inscribed inside of the triangle. Therefore, we can find a circle with the incenter and radius
of length equal to the distance of all three triangles sides. Even though these definitions should
simple, their construction can be very tricky.
Let us first
discuss how to create the circumcenter.
Since we have to find the perpendicular bisector of all three sides of
the triangle, we must first discuss how to create the perpendicular bisector. A perpendicular bisector is the line
that intersects another line segment at a 90 degree angle with equal distance
from both of its endpoints. To
simplify this creation, let us name the line segment that we are intersecting
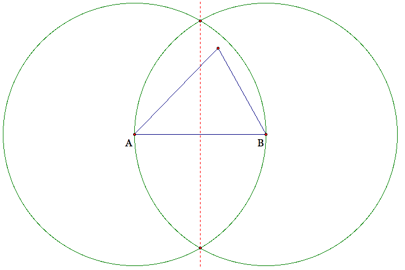
line segment AB. To create this bisector,
we must first create a circle with the center at A that intersects the point
B.
Then we will create a circle with the center at B
that intersects point A. Since
both of these circles have the same radius length of AB, the intersection of
these circles will have distance of AB from both points A and B.
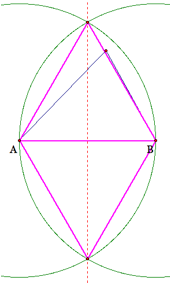
As we can see from the picture below, this
creates two equilateral triangles, and the vertices that coincide with the
intersecting circles create a line that bisects our equilateral triangles. This
produces four congruent triangles from our two equilateral triangles. We know the bisected angle will be 30
degrees (since it is was original the 60 degree angle) and the original side
angle is 60 degrees (from the equilateral triangle), thus our red line intersects
the line segment AB at a 90 degrees angle. This shows that we have now created our perpendicular
bisector.
We must duplicate this process on each of the
three sides of the any triangle.
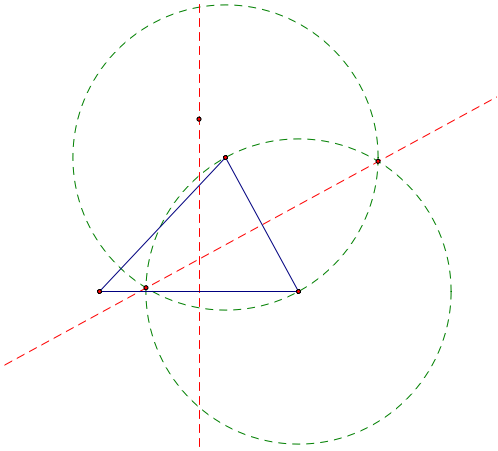
Once we have the three perpendicular bisectors,
we need to find the intersection of those three lines which is our
circumcenter.
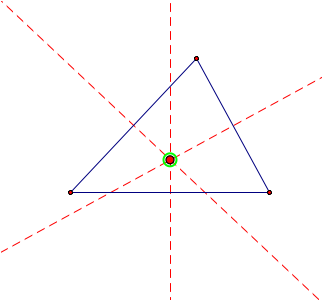
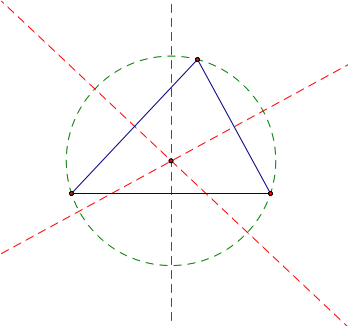
We can prove that this point is a circumcenter by
creating a circle from that point which connects all three vertices as seen in
the picture below.
Now, let us discuss
the construction of the incenter.
We already know that the incenter is created by the intersection of the
angle bisectors of each angle of our triangle. However, how do we construct an angle bisector which is a
line that bisects the angle? To
create this shape, we must first create a circle from one of the vertices of
the triangle that intersects two of its sides.
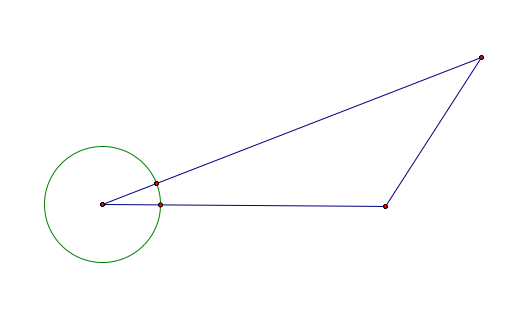
As well can see from the picture, we now have
found two points on the rays of that angle that have equal distance from our
vertex. Therefore, to find the angle bisector we must us those two
new intersections as centers of two new circles that both intersect the
vertex.
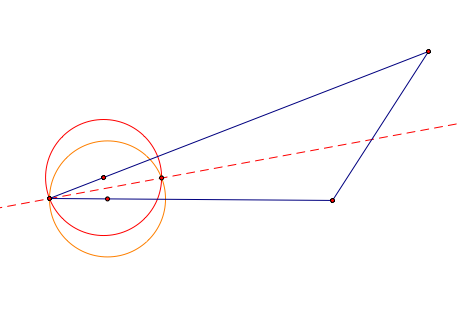
We constructed these two circles to have the same
radius length. Therefore, we know
the distance from DA = AC = BC = BD.
From this information, we know that we created a rhombus inside our
triangle. We know that the
diagonal bisects the angle of the rhombus, thus we have an angle bisector of
angle D.
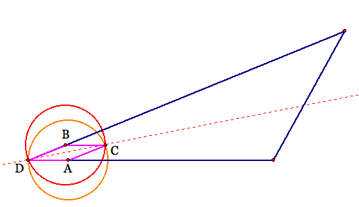
We
must create this angle bisector on all three sides.
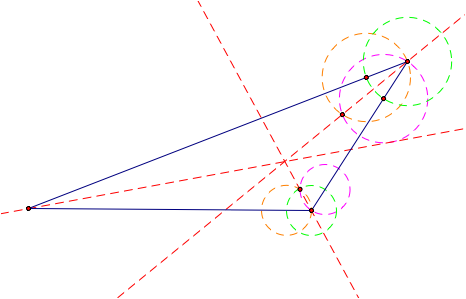
Once we have all three lines, the incenter is
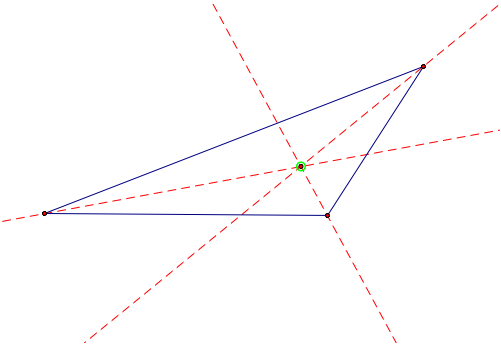
very easy to find.
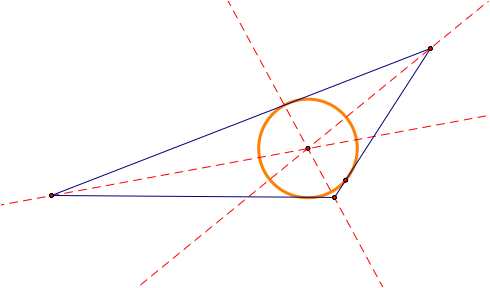
To prove that intersection was the incenter, we
can create the inscribed circle with that center with the circle touching each
of our three triangle sides as seen in the picture below.
These
constructions are very hard to create by hand because of the need for complete
accuracy of each one of our circles.
If the distance of any of the circles’ radiuses where skewed by a shaky
hand or a difficult compass, the incenter and circumcenter would not create
their respective circles.
Therefore, we using the Geometers Sketch Pad the students can construct
accurate pictures with reliable results.