Tools for
GSP
By: Amanda Sawyer
This document consists of many great new tools for Geometerís Sketchpad. Click on any of the links to see the script and tool in use inside GSP.
|
Tool and Definition |
Image |
|
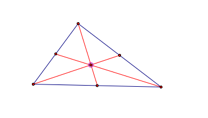
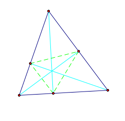
Centroid: Given any three points, this application will create a central point from the segments connecting the midpoints of each side to its opposite segments vertex. |
|
|
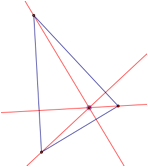
Orthocenter: Given any three points, this application will find the intersection of the lines created by the three altitudes. |
|
|
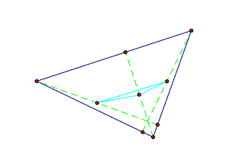
Orthocenter Triangle: Given any three points, the midpoints of the line segments from the orthocenter to the vertices of the given triangle will create a triangle. |
|
|
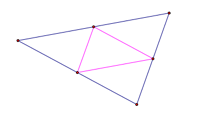
Medial Triangle: Given any three points, this application will create a triangle from the midpoints of all three sides of the given triangle. |
|
|
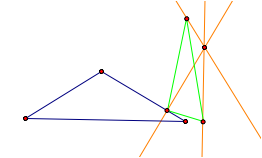
Orthic Triangle: Given any three points, this application will create a triangle from the feet of the altitudes of the given triangle. |
|
|
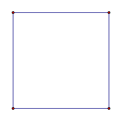
Square: Given any two points, this application will create a quadrilateral with four sides of equal length and four angle of congruent measure. |
|
|
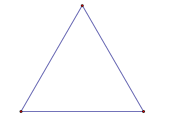
Equilateral Triangle: Give two points, this application will create a triangle with equal sides length and congruent angle measure. |
|
|
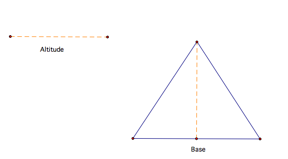
Isosceles Triangle: Given a base and an altitude, the application will create an isosceles triangle. |
|
|
Pedal Triangle: Given any four points, this application will create a triangle and a pedal triangle from the given fourth point. |
|
|
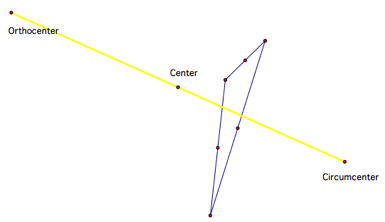
Eulerís Line Segment: Given any three points, this application will connect the triangles orthocenter and circumcenter which is our Eulerís Line Segment. The midpoint of our Eulerís Line Segment is the center of the nine point circle. |
|
|
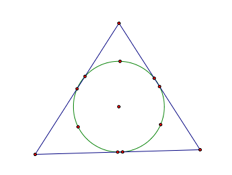
Nine Point Circle: Given any three points, a circle is created from the midpoints of each of the triangles sides, foot of each of the altitudes, and the midpoint of each line segment from the orthocenter to a vertex. |
|
|
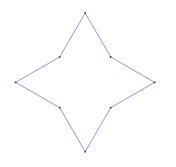
Square Stellation: Given any two points, this application will create a star created from a square and four equilateral triangles. |
|
|
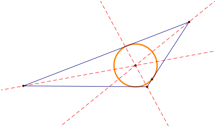
Incenter: Given any three points, this application will find itís incenter and its inscribed circle |
|
|
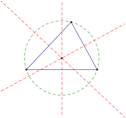
Circumcenter: Given any three points, this application will find itís circumcenter and its circumscribed circle. |
|
|
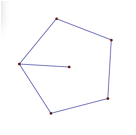
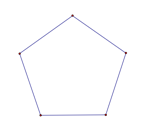
Pentagon (Given a Radius): Given a radius, this application creates a regular pentagon. |
|
|
Pentagon (Given a Side): Given a side, this application creates a regular pentagon. |
|
|
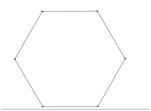
Hexagon (Given a Side): Given a side, this application creates a regular hexagon. |
|
|
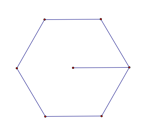
Hexagon (Given a Radius): Given a radius, this application creates a regular hexagon |
|
|
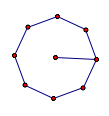
Octagon (Given a Radius): Given a radius, this application creates a regular octagon. |
|
|
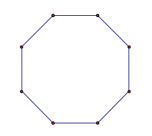
Octagon (Given a Side): Given a side, this application creates a regular octagon. |
|