
Equal Distance Between and On Rays
By: Amanda Sawyer
Given three points A, B, and C, we are asked to construct a line intersecting AC in the point X and BC in the point Y such that
AX = XY = YB
We want to prove that this property is valid without using measurements or dragging elements in GSP. The best way to show this property within an angle is by using the fact that a point will have equal distance to a center on any circle. Let us consider this figure ACB,
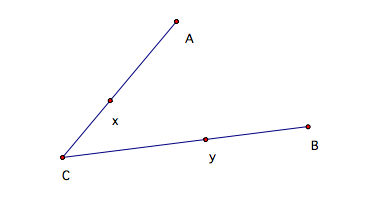
In this assignment, we want to show that the distance between X and Y is the same as the AX and YB. Therefore, lets connect XY to see what kind of properties we can find.
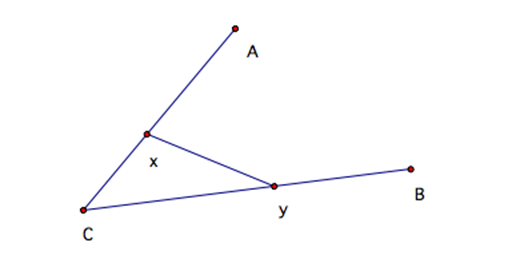
We want to show that the segments XY=AX=YB by using different properties of geometry. Let us pick X to be an arbitrary point between AC. Let us set x as the center of a circle with radius of distance XA. By the definition of a circle, we know all points on the edge of the circle are equal distance away from the center. Since A and Y are both on the circle with center X, we can clearly see that the distance from XA=XY.
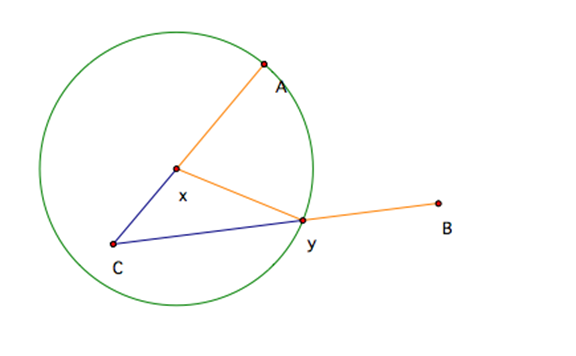
Now, all we need to show is that XY has the same distance of BY. To do this, again we will construct another circle, but this time the center will be Y and the radius distance will be XY. Again, it is clear that the point X and B are both elements on the edged of center Y.
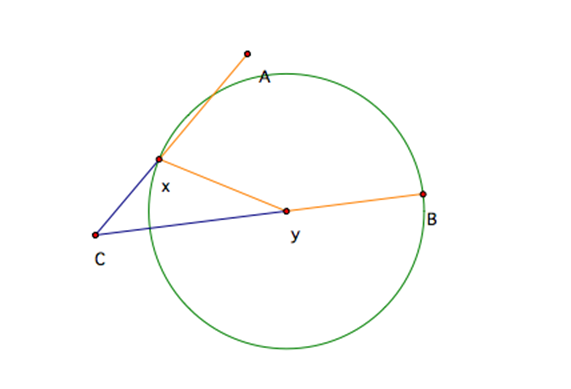
Therefore, we know that XY=BY. Since AX=XY and BY=XY, thus by the transitive property we the segment AX=BY, and AX=BY=XY. This kind of property is very unique to this shape. These triangle ABC was constructed with the above properties to attain the given shape. We create this shape by first defining a line AC with a X value in between A and C.
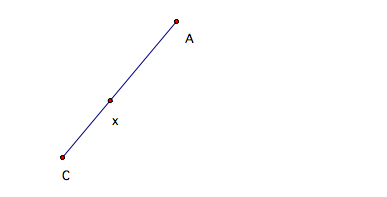
Since we want XA=XY, we must define a circle with center X and radius A to have a point Y.
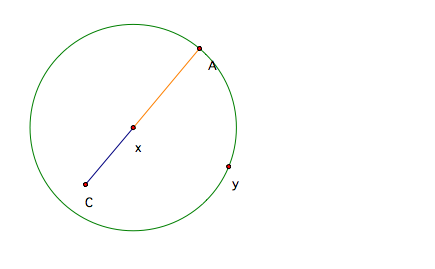
Now, we can connect XY and CY to create part of our figure. However, we still do not have the point B.
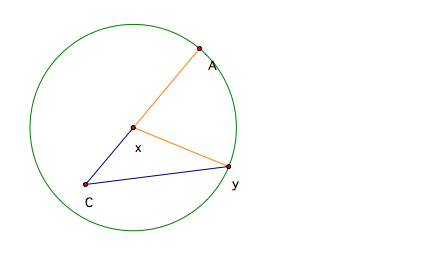
Since we need the property that YB=XY, we again will create a circle. This time our center will be at Y with radius XY. We know that the line segment CB will contain the line segment CY, so we will extend the line of CY to find where B lives on the circle we just created.
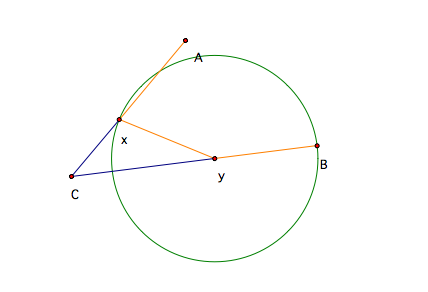
This creates the shape that will give us the property AX = XY = YB.