Tangent Circles
By: Amanda Sawyer
In this assignment, we are asked to study what happens to the center of a circle when it is tangent to two other circles.† In this investigation, we will look at two circles tangent circle when A) the tangent circle connects the inside of our two original shapes and B) the tangent circle connects the outside of our two original shapes.
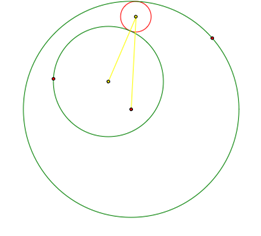
A) INSIDE TANGENT CIRCLE
First letís consider the tangent circle created by the two circles with tangents located in the inside of their shapes.† When we study this circle, we create this shape by first creating two circles and then picking an arbitrary point on one of the circles.† Once we have made the line segment connecting the center of our circle and the arbitrary point on that circle, we only need to add the distance of the other circle to find our length of our first line.† From that endpoint, we will create a line segment to the center of the other circle.† Then we will create the perpendicular bisector from each that segments midpoint.† This line intersects the radius of our original circle which becomes the center of the tangent circle.† With the center and the radius, we are able to create our new shape.
Now we can study what happens to the center of our tangent circle when it is rotated around the original shape. Notice that the center creates an elliptic shape and a hyperbolic shape shown in our picture below in yellow.
|
Case |
Picture |
|
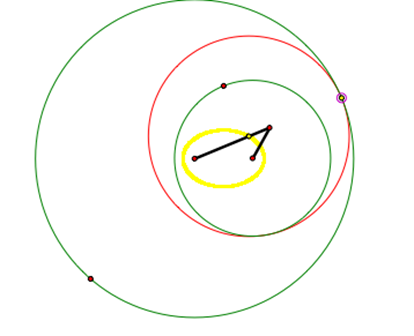
1) When one circle is inside the other circle, it
creates an ellipse from the trace of the center of the tangent circle. |
|
|
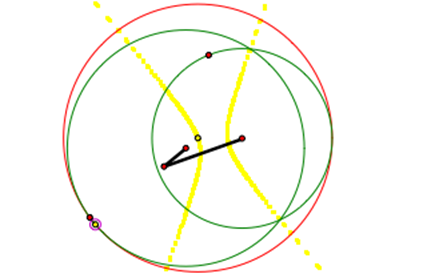
2) When one circle intersects the smaller circle at
two points, it creates an ellipse from the trace of the center of the tangent
circle. |
|
|
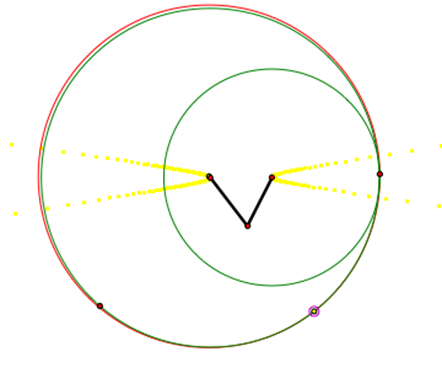
3) When one circle of equal size intersect the other
circle of equal size at two points, it creates an ellipse from the trace of
the center of the tangent circle. |
|
|
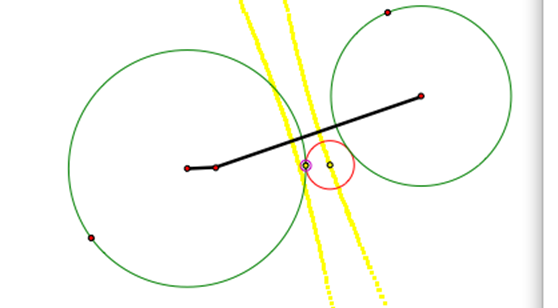
4) When the two circles are not connected, it
creates an hyperbola from the trace of the center of the tangent circle. |
|
|
5) When the two circles intersect at one point , it
creates an hyperbola from the trace of the center of the tangent circle. |
|
We notice in the first three cases shown above have the trace of the center of the tangent circle creating an ellipse and the last two cases trace creates a hyperbola.† We can understand why this occurs when we consider the construction of these shapes. It is easy to see that the sum of the distances from the center of the first circle to the center of the tangent circle and the center of the second circle to the center of the tangent circle will always be the same. This property is show in yellow in the pictures above.† The yellow line is created by the radius of the larger circle combined with the radius of the smaller circle.† That is why the value always stays the same.† Therefore, when our two circles have two intersections, the trace of the center of the tangent circle creates an ellipse.† When the two circles have one intersection with one circle located inside the other circle, it creates an ellipse.† For all other cases, the distance between the two circle centers is so large that it creates the hyperbola from the trace of the center of the tangent circle.
†
B) OUTSIDE TANGENT CIRCLE
Now letís consider what happens when we create a tangent circle from the outside of two circles.† When we construct his circle, we will first construct a circle and then another circle within it. Then we will create a line through the center of the larger circle. Next, we will create a circle with the center at the intersection of the line and the radius the same as the smaller circle. After you have created the circle, then construct the midpoint between the center of the smaller circle and the intersection of the line and the constructed circle, outside the larger circle. When the midpoint has been created, construct the line through the midpoint that is perpendicular to that line. The intersection of the perpendicular line and the line through the center of the circle is the center of the circle that will be tangent to both circles. To find the radius of the tangent circle you must use the distance between the center of the circle and the center of the constructed circle. This gives you a circle that is tangent to both of the original circles.
Now we can study what happens to the center of our tangent circle when it is rotated around the original shape. Notice that the trace of the center creates an elliptic shape or a hyperbolic shape shown in our picture below in yellow.
|
Case |
Circle |
|
1) When one circle is inside the other circle, it creates an ellipse from the trace of the center of the tangent circle. |
|
|
2) When one circle intersects the smaller circle at two points, it creates an hyperbola from the trace of the center of the tangent circle. |
|
|
3) When the two circles intersect at one point , it creates an hyperbola from the trace of the center of the tangent circle. |
|
|
4) When the two circles are not connected, it creates an hyperbola from the trace of the center of the tangent circle. |
|
†††††††††††††††††††††††
We can notice in this picture that the trace of the center of the tangent circle is hyperbolic in three out of the four cases.† We can see that the only way for our trace to be an ellipse is when there are no intersections between the two circles and one circle is contained inside another circle.† In all other cases, we can see that our trace creates the hyperbolic shape.† Again, we can see that this is true because the tangent circle must get larger and larger until it reaches infinite length to stay tangent to both circles.
Through this investigation, we were able to study tangent circles and the characteristics of its trace using the tools in Geometers Sketchpad.† From this software we are able to explicitly see what happens when our radius is infinitely large.† From this information, we can make assumptions about our shape that is much more difficult to do by hand.