
A Proof of the Nine Point Circle
By: Amanda Sawyer
We can create the circle given nine distinct points on a triangle. The first three points are the feet of the altitudes of our triangle with the name of D, E, and F. The next three points are created from the midpoints of each of the triangles sides (G, H, I). The last three points are from the midpoint of each line segment from the orthocenter to a vertex (J, K, L). I want to prove that points D, E, F, G, H, I, J, K and L are all contained on the same circle.
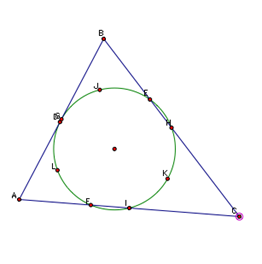
Proof:
In any triangle, we know that the line that connects the midpoints of two sides of a triangle is parallel to the opposite side. Therefore line segments GH and AC are parallel as seen in the picture bellow.

We also are told through the construction that L and K are midpoints of the lines segments connecting the orthocenter to the vertex. Therefore, we now have line segments GH, AC and LK being parallel.
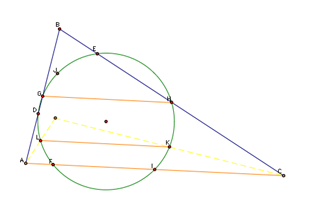
With this same logic, we can see that we can make a new triangle B, incenter, and C such that by the midpoint theorem, the lines B and the incenter are parallel to HK.
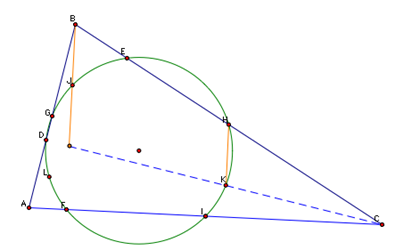
Also, we can look at the triangle created by the incenter B and A, and see that we also have two parallel lines LG and B with the incenter. Therefore by the transitive property, it is clear that we know have proven that GL and HK are parallel.

Now, we can see that we have a parallelogram created from GHKL. Since the perpendicular line creates the altitude of any triangle, we also know that each angle of our parallelogram is ninety degrees, therefore we have a rectangle. Since the opposite angles of this quadrilateral are supplementary, we can see that this rectangle can be inscribed in a circle.

Using similar construction, we can see that another rectangle can be created from these points.
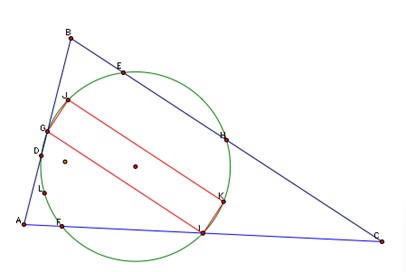
From this information, it is clear that points J, G, D, L, K and H all exist on the same circle. This circle has diameter JI since it is diagonal to both rectangles. Therefore its midpoint is our center, and we will name it O. Now we must show the last points E, F and D are also on this circle. Since F is the foot of our altitude, it creates a ninety-degree angle for the triangle JFI, thus F must be on our circle.

Similarly, we can see that H is in the circle because it too creates a ninety-degree angle with its triangle IHJ.

Finally, we can see that D is also on the circle because it creates a ninety-degree angle with its triangle JDI.

Therefore, we have seen that all nine points are located on the circle, therefore the nine-point circle exists for any three points ABC.
NOTE: This proof was adapted with assistance from the Computer Science and Mathematics Department of Arkansas State University