Here is the investigation on plotting polar coordinates

by

Ryan Shannon

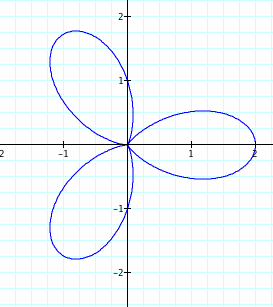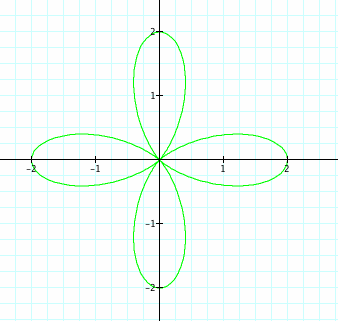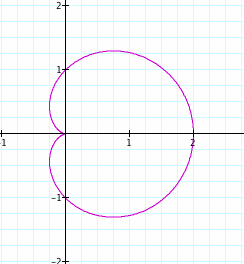
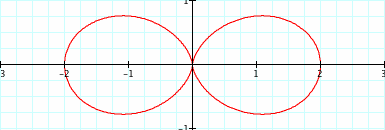
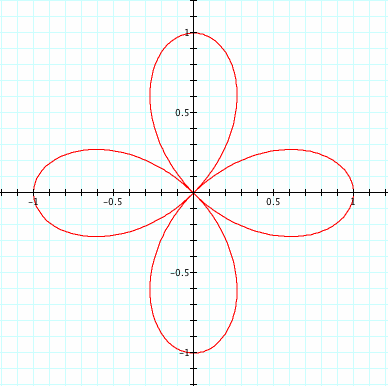
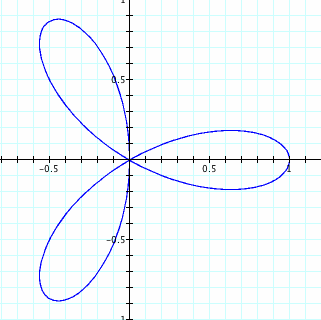
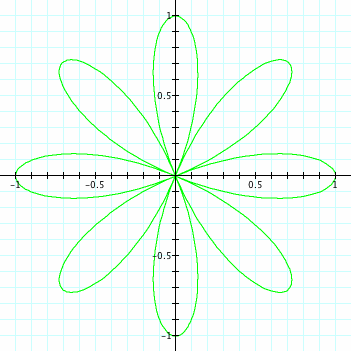
After plotting the points in graphing calculator we notice that the "K" in our equation, changed from 1,2,3,4 respectively. As K increases so does the amount of Petals in our graph. Note: a,b=1 Click below to see just how k changes the amount of pedals and direction in which the pedals from, this will be important later.

Would anything strange happen if we change a, and b. how will these effect the graphs?

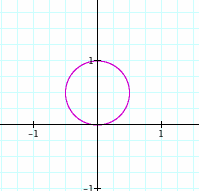
Lets us fix k=4 and a,b=1

When 1<n<3 the graph represented by purple have a flower look, with a red barrier. We have four addition pedals to our function. When looking at more graphs we notice that this phenomena will double the pedals in all graphs. the pedals will be 2k when k is fixed. We see that the pedals peak at the n value plus one. As cosine has a range of -1 and 1

That is that When -3<n<-1 in the graph the graphs will swap with one another. Thus red will be purple and vise versa.

Strange, now that we have removed our constant a, and then our even graphs now have 2k pedals. Also our domain, dropped from (-2,2) to (-1,1).

Clicking the equation above we can see a few things. We notice that when n is a coefficient only the size of the pedals have changed, because cos will stay constant at one thus, the arcs will peak at the value of n.

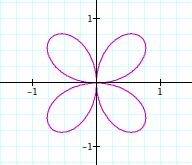
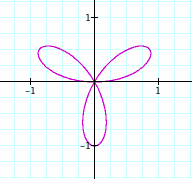
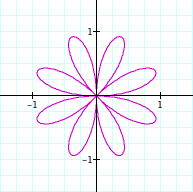
We notice here that when bringing n to theta that not only is the amount of pedals changed drastically but the direction is changed too. When n is positive we move about the origin counterclockwise similar to the way we graph in the unit circle. When n is negative we rotate about the origin in a clock-wise direction. Also we are able to prove and show that the amount of pedals for even n will be 2n and n for odd. We can see that when n is odd that the two pedals are over lapped by one another.

Here we now change from cosine to sine, and see how the "rose" changes.

We already know that sine and cosine have a phase shift of pi/2 from one another.

As cosine is 1 at 0, n*pi. Sine is 1 at Pi/2 *n

Thus when we are looking at the graphs below we notice that they are very similar to cos but rotated. The direction that the pedals are formed is the opposite of cosine.

It looks like as the number k is the corresponding rotation from cosine to sine by pi/2k. As in when k=2 the graphs will be shifted from one another by pi/4

We also notice that b will effect the sine pedals same as it has above in cosine.

The same properties will hold for sine if we reintroduce the constant a value.

To see for sure how things are similar and different from cosine click the link below.

Home