


Is Fibonnaci thinking golden?
Taking a look into the fibonnaci sequence through Microsoft Excel
By
Ryan Shannon
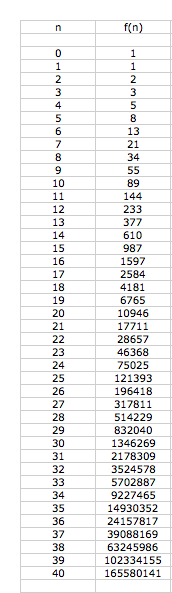
Each value is created from adding the previous f(0) =f(1)=1 and f(n)=f(n-2)+f(n-1)
Looking at the sequence we find the ratios of the original from the continuing values. We notice that f(n+1)/f(n) looks to be pretty golden.
Can we prove this?
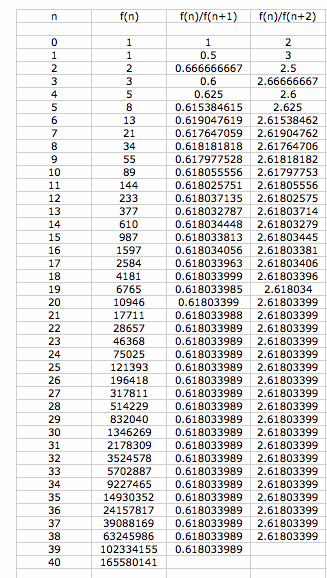
If we look at the ratios that is f(n+1)/f(n)
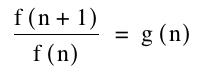 |
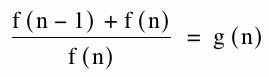 |
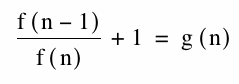 |
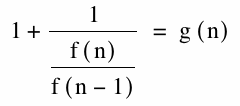 |
We notice that our last step will reveal that we have;
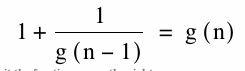
We know that g(n) and g(n-1) if they converge, will converge to a number call it x, will converge to the same number when approaching infinity.
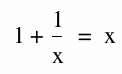
This looks very familiar. I'm thinking we have found something there.
![]()
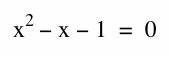
If we are to use the quadratic formula we find
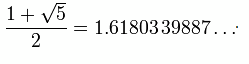
Eureka! We are golden!
If we step back to our excel spreadsheet above, we notice that the next ratio is 2.618033... which is the golden mean +1!
Then we being to worry, will this work for any value of f(0) and f(1)?
If we let f(0) = 1 still and change f(1) = 3, f(1) = 7, and f(1) = 9
As we can see by the Excel chart that the ratios will stay the same.
After all this investigation I'm think these ratios have the midas touch