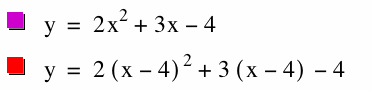Transfixing Transformations of Quadratics
A look at:
By Ryan Shannon
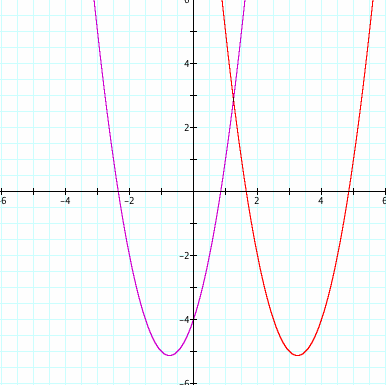
Here is a way to show that the shift is only applied to the x-values. We find that both -values are equal. When choosing the point to find a vertex, we know that the x-coordinate will be x= -b/2a. Thus, by using this equation we can find that the vertex will be the same for both quadratic equations.
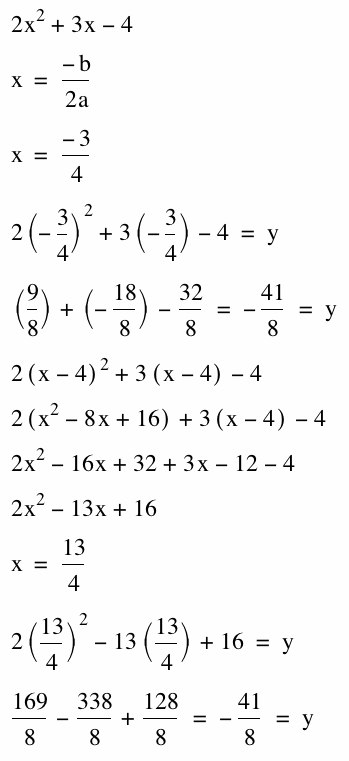
We can clearly see that f(x-4) will only effect the x-coordinates. Y-values will remained unchanged. This is a translation.
First given an equation in standard form Seeing this equation above we notice that when dealing with 
the standard value of a parabola with vertex given. Value h, will translate the problem left or right. We notice that when the from x-h the function moves h-units to the right, or the "opposite" direction.
We notice that too, the range will remaining the same. The domain too will remain the same.
We should take this a step further and test our hypothesis and see if the same would be true for (x+h) where x values would be shifted left h-units or "opposite" direction.
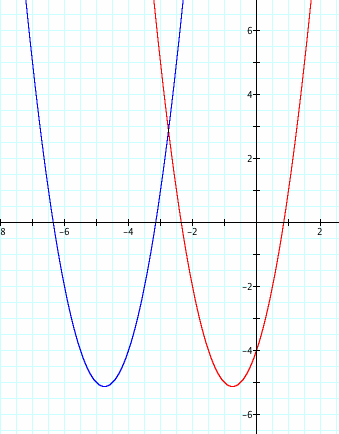
Seeing the graph above we can tell that our assumption was true. When wanting to shift a graph left or right, it is necessary to place the operation within the x-value.
Now we have explored what happens when changing the values of x, what if were are to change the value outside x, or the coefficient of x to a negative number.
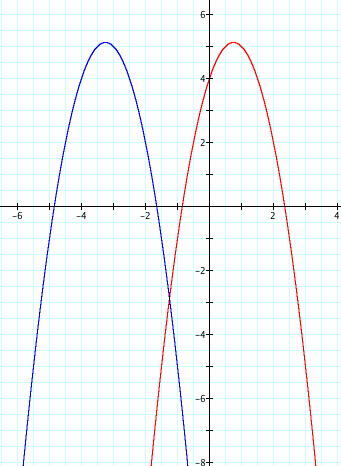
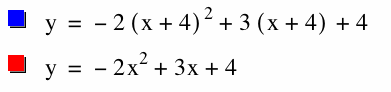
Noticing the graph above we are able to see that the shift now (x - h) is maintained, the major change is the direction of the graph itself. The graph has been "flipped" or reflected over the axis of the x-value of the vertex. The properties of the translations will remain the same. That is F(x-4) will translate the x-values of the graph right 4-units.
We can not the the range will be negated as well. Range= [4,infinity) will now be (-infinity,-4]. Domain will be unchanged in both cases.
Now that we have translated on the x-axis we need to investigate how to translate on the y-axis.
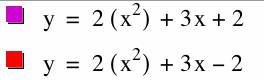
If we are to change the values of c. in our cognitional equation, will this create a vertical shift?
We claim that c is the y-intercept of the graph. By looking below we notice that the shape of the graph is unchanged.
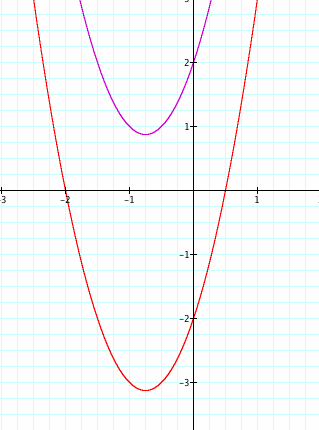
We we expect, this has created a vertical shift. This vertical shift is also in aggreance with sign of c. This is different than a horizontal shift that was the opposite sign.
The domain will remain unchanged again, where as the range will very as c varies.
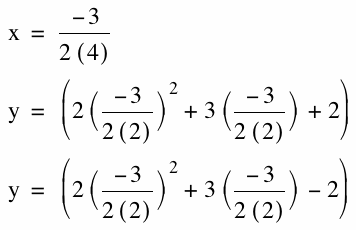
When using the x=-b/2a method for finding the vertex we notice that the vertex will be shifted up 2 and down 2 from the x-axis. In turn, we will have a change in only domain that will be from the corresponding y-coordinate to infinity.
There is no need to investigate that will happen as we negate the coefficient of a as we did above, knowing that vertical shift will be constant to the horizontal shift above. No matter if this is a negative of positive parabola, translations will be preserved.
If you're interested in how the graphs will move horizontally and vertically; click below.
An interesting note is that when the positive parabola has zero real roots, the negative graph will have zero real roots are the additive inverse
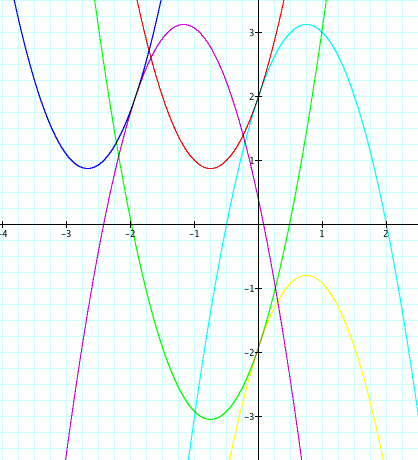
What if combine the following functions above.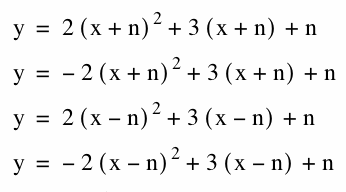 
When looking at the four transformations above we can label them 1,2,3,4 respectively. We notice that in equation 1 and 2 the (x+n) will shift the graph on the x-axis left and the +n will shift us up on the y-axis when n>0. And the opposite when n<0. The graph will be moving along the y=-x. Also the equations 3 and 4 will be translated positively in both x-axis and y-axis when n>0 and negatively when n<0. Therefore they will transform along the y=x line.
To see how this will be changed in the XB-plane click here