This point, that point, in the end, we're all the same.
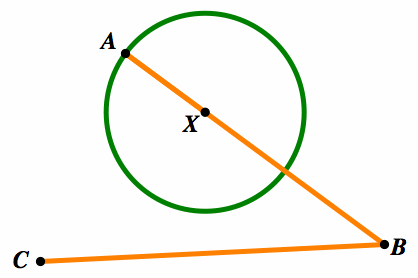
When Given three points A,B,C Find a point on line AC called X and another point on BC called Y
AX=XY=YC
By Ryan Shannon
As we start the investigation we will pick an arbitrary point X on AB and make our circle radius the measure of AX centered at A, thus our circle will change with respects to the post ion to X
If you seek a more interactive investigation, please click the photo for how the circle will change as the position of X changes on AB
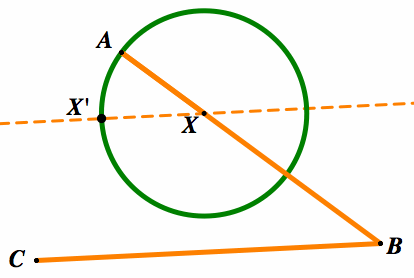
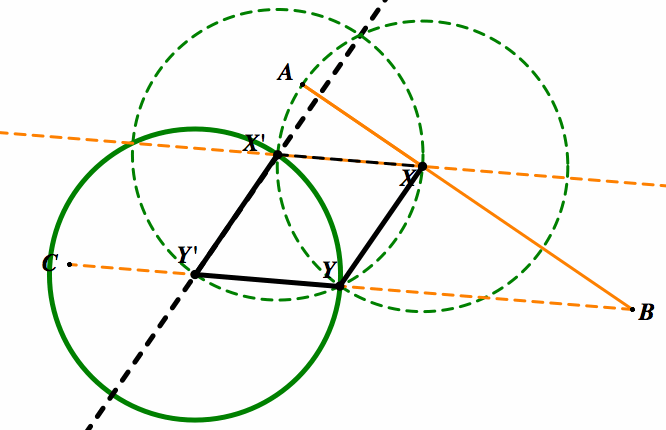
Here we have drawn a line parallel to BC passing through X, we have labeled the interior intersection as X'. It is obvious that the length of XX' will be equal to the length of AX as both are radii to the circle. The reasoning for this step will be made clear in the next construction.
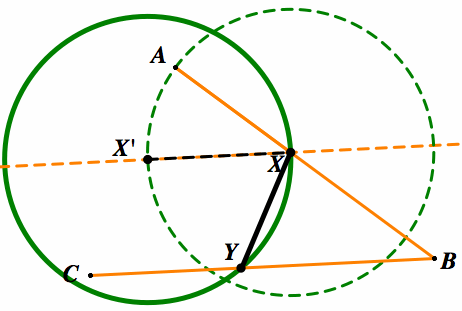
Here above, we have shown the value of the first circle by creating another circle with radius length XX' centered at X. This will prove to be very useful as we are now able to create XY that is the same length as AX.
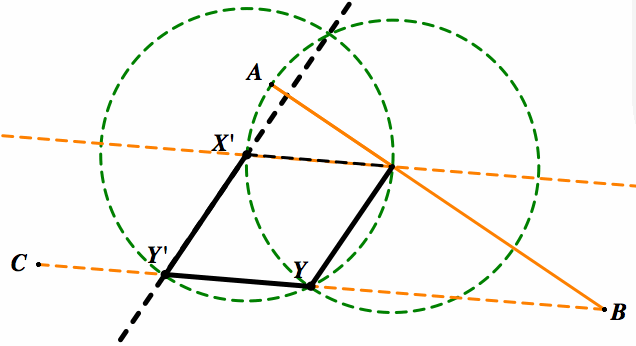
Here we have created a line parallel to XY passing through the point X'. To create this we had to extend line BC to that we can ensure that X'Y' will intersect the line. As X'X and BC are parallel to one another, we know from Thales Theorem that the point Y' will be the same length as XX'.
Now to show again as we can see the circle centered at Y' with radius length X'Y' intersects Y. Which is the same length as XY equal to X'X and is equal to AX. By having circles of equal radius lengths we can prove this.
Showing that
AX=XY=YY'
Since the points are dependent on X, we can arrange all our points from the point X. I have placed another interaction link above to see how all the points change with respects to the point X.