The light touch of a Tangent Circle
By Ryan Shannon
When looking at two circles and the tangent to both of them we will have two cases. We will call the Case 1 "smaller" case.
Here we will try to make a connection to each circle that is tangent to another.
Case 1 Disjoint From Another
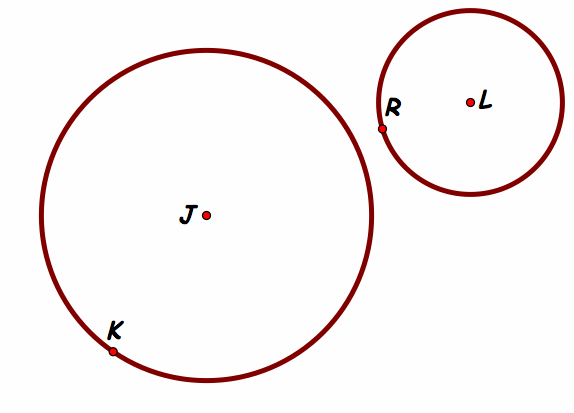
Part A.) The "smaller" Tangent (Use image to get GSP for other investigations.)
Given Two circles, one with radius JK the other with radius LM we must find a circle tangent to both.
Description: As we are given circle J and circle L we construct another Circle, N where the radius of circle N is the length of LM, or radius of circle L. Thus NO=LM. From this we construct a line from O to L.
We can use this line to find an equal distance from the edge of each circle. After construction of OL, P is the midpoint, and QP is the perpendicular bisector of LO. Now by SAS we can show that LQ=QN, from this we get LR=ON then we can see that circle Q with radius QN will be tangent to both circles given.
Part B.) The "larger" Tangent
Given Two circles, one with radius JK the other with radius LM we must find a circle tangent to both.
Description: As were are given circle J and circle L, we construct another circle, K where the radius of K is the length of LM or radios of circle L. Thus KO=LM. From this we construct line LO.
We can use this line to find and equal distance from the edge of each circle. After construction of LO, P is the midpoint. PQ is the perpendicular bisector of LO. Now by SAS we can show that OQ=LQ and OK=LM then KQ=QM By this we know that the circle Q with radius QK will be tangent to both circles.
Investigation: In this tangent case I noticed that both circles are inside the tangent.
Case 2 Inside Another
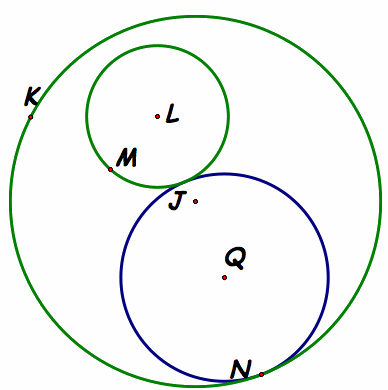Part A.) The "smaller" Tangent
Description: The construction that is cone here is the same as done above. Thus all the work can be done by using the "smaller" gsp link from the photo above.
Investigation: Here we notice that the tangent circle is encompassed inside on circle.
Part B.)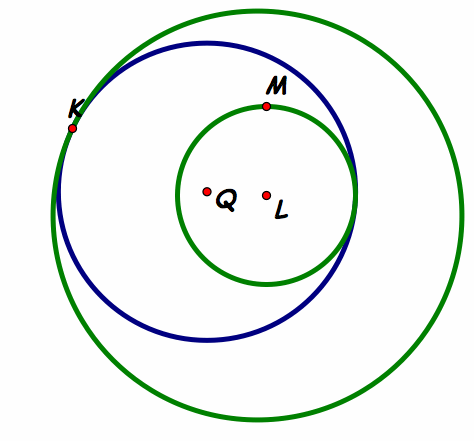 
The "larger" Tangent
Description: The construction that is cone here is the same as done above. Thus all the work can be done by using the "larger" gsp link from the photo above.
Investigation: Here we notice that one circle is completely encompassed in the tangent.
Case 3 Over Lapping Another
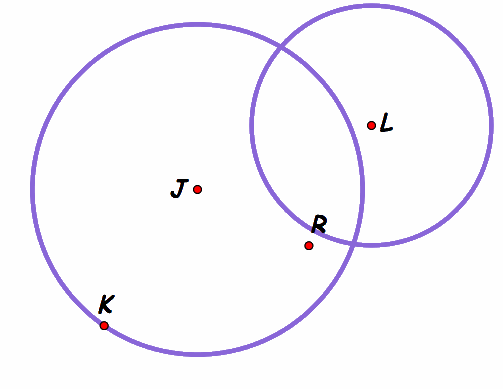
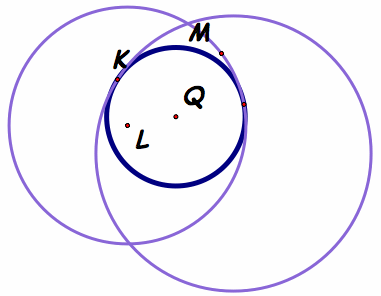Part A.) The "smaller" Tangent
Description: The construction that is cone here is the same as done above. Thus all the work can be done by using the "smaller" gsp link from the photo above.
Investigation: Here we notice that the tangent circle is encompassed by both circles.
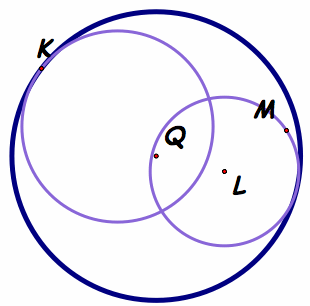Part B.) The "larger" Tangent
Description: The construction that is cone here is the same as done above. Thus all the work can be done by using the "larger" gsp link from the photo above.
Investigation: This shows that both circles are inside the tangent circle.