

Pedal To the Medal
An investigation on the Pedal Triangle and a few neat tricks it may entail.
By
Ryan Shannon
Given a Standard Pedal Triangle
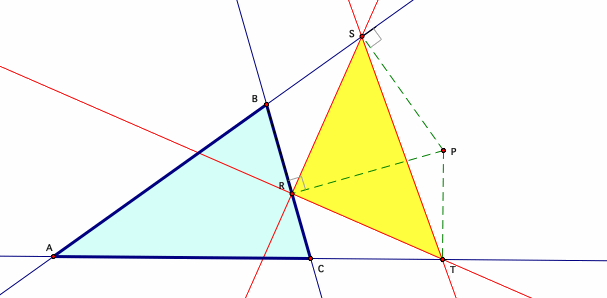
What would happen if we placed point p as the centroid of the original triangle ABC. This triangle consists of points R, P, T that are the intersection points of the lines perpendicular to the pedal point and the lines of the triangle ABC. A pedal point can lie outside or inside the original triangle ABC as well as being on one of the lines of the triangle ABC.
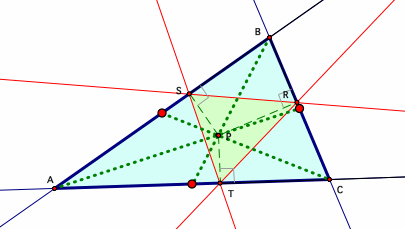
To the looks of the photo there must be come relation to the pedal triangle and the original triangle ABC.
If we are lucky enough to to get the pedal point to be the same as the inceter, this will have the circumcircle of the pedal triangle.
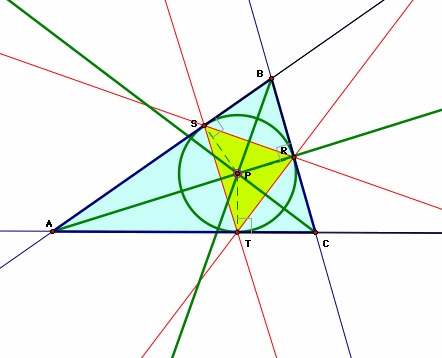
What if the point of the pedal triangle are collinear? Does this create anything?
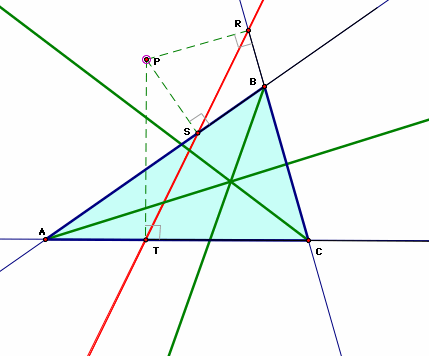
Seeing that R,S,and T are collinear we have created the Simson Line
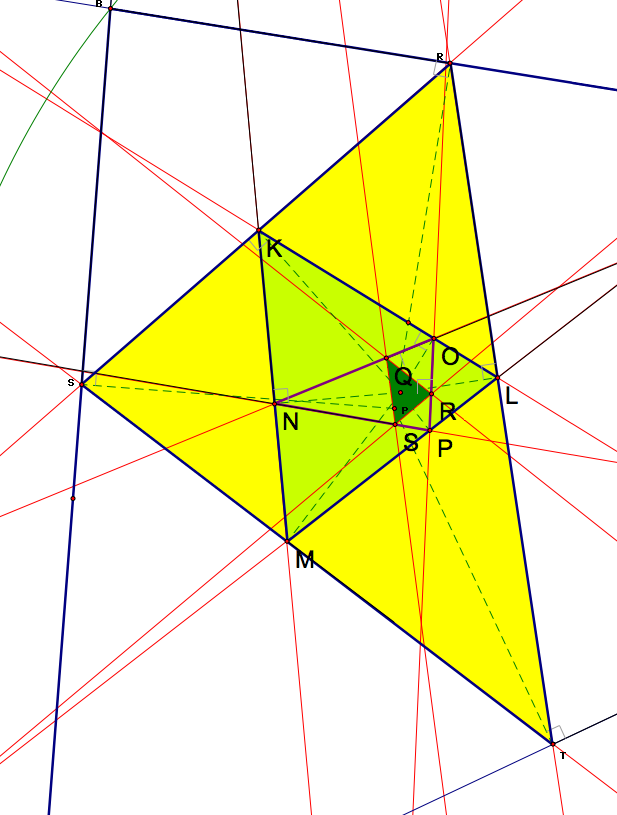
You may think I'm weird or a person with too much time on their hands but lets look at the pedal of a pedal of a pedal.
Here we notice something strange has happened.

Crazy! The investigation on how to prove that these triangles are equal is done from circumcircle of each triangle.