The Grand Finale

We investigate the ratio:

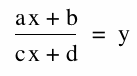
And equate asymptotes, domain and range, and see how changing each will be effected differently.

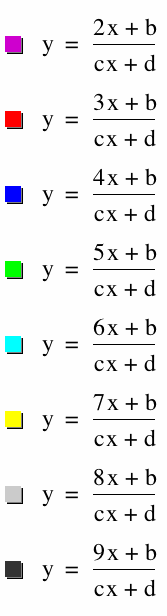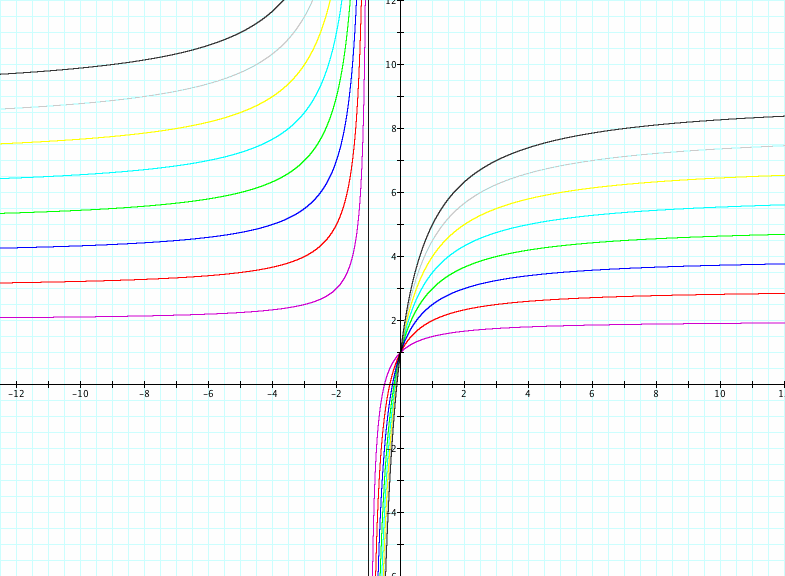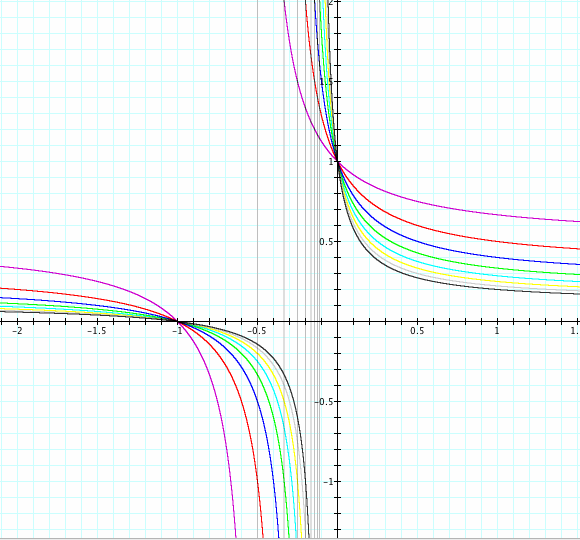
Above we change the value of a from 2,9 and notice that there is a horizontal asymptote at the corresponding a value.

We can see right away that if we let x=0 the y-intercept will always be 1. thus all the graphs pass at (0,1).

It seems that the horizontal asymptote is going to be "a" can we prove this?

Let b,c, and d =1 and let a=2

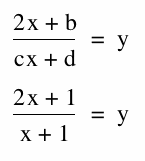
So if we take the limit as x approaches infinity, we will get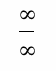

thus we will take the derivative of both the top and bottom but L'hopital rule.

Here we notice that the horizontal asymptote will be for each changing a and correspond to the value of a.

Thus we will have a horizontal asymptote at

All other horizontal asymptotes will follow suit.

Well why do all the graphs above share the same vertical asymptote?

This is what values will not work in the range, given our domain. We know our domain is going to be .

So which values will make our equation explode? That is when the denominator equals 0. This will happen in every graph when

Thus we have a vertical asymptote at the value

Here we notice that our range will be

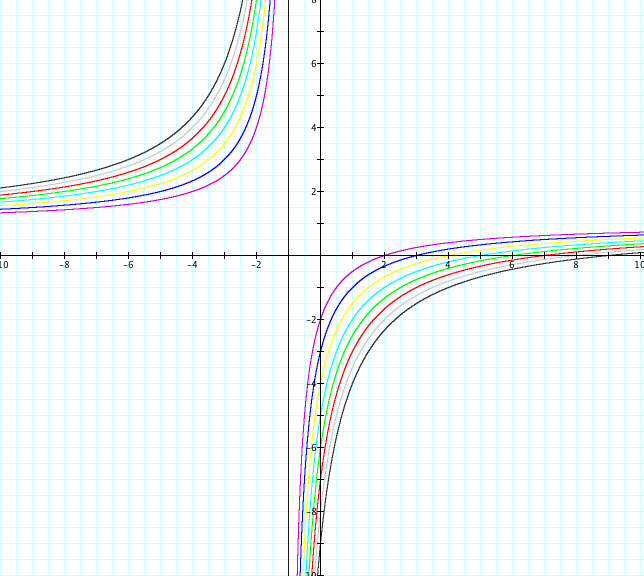
Below we change the value of b from 2,9 and investigate the horizontal and vertical asymptotes and domain and range.

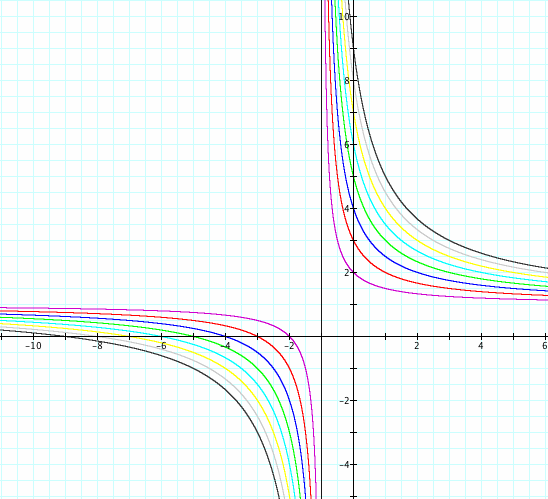Above we change the value of b from 2,9 and notice that there is a horizontal asymptote at the corresponding a value.

If we left x=0 then we will have a y-intercept that is corresponding to c.

It seems that the horizontal asymptote is going to be "a" can we prove this?

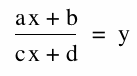
Let a,c, and d =1 and let b=4

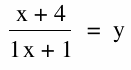
So if we take the limit as x approaches infinity, we will get

thus we will take the derivative of both the top and bottom but L'hopital rule. We get 1.

We see here that the horizontal asymptote will be

If we look closely at the graph above we see that the vertical asymptote is similar to the one when we were changing the value of a.

This is what values will not work in the range, given our domain. We know our domain is going to be .

So which values will make our equation explode?

That is when the denominator equals 0. This will happen in every graph when

Thus we have a vertical asymptote at the value

Here we notice that our range will be

This is interesting to not that c looks to only effect the y-intercept of a graph.

Here we are changing the values of c. Is this going to change our asymptotes? Will this change our domain and range of the functions?

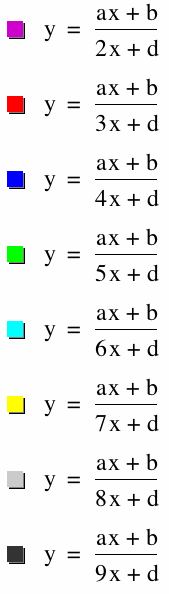Let x=0 we get that all graphs will have y-intercept of -1 or 1. Thus all graphs pass (0,-1) or (0,1)

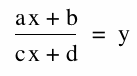
Let a,b, and d=1 and let c=3

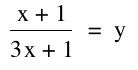
To find the horizontal asymptote;

We take the limit as x approaches infinity, we will get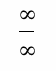

thus we will take the derivative of both the top and bottom but L'hopital rule.

Here we notice that the horizontal asymptote will be for each changing c and will correspond to the value 1/c. As the other horizontal asymptotes will follow a similar process.

Well why do all the graphs above share the same vertical asymptote?

This is what values will not work in the range, given our domain. We know our domain is going to be .

So which values will make our equation explode? That is when the denominator equals 0. This will happen in every graph when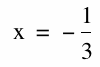

Thus we notice that the vertical asymptote will be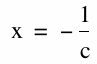

and the range will be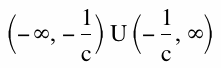

Here we are changing the values of d. Is this going to change our asymptotes? Will this change our domain and range of the functions?

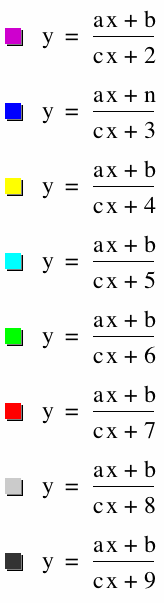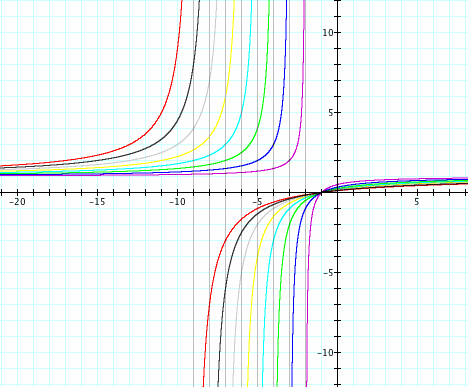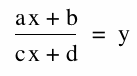
If we let x = 0. We will get a y-intercept of 1/d that is (0,1/d)

If we let y=0 that we get the x-intercept of -1. Thus (-1,0)

Let a,b, and c=1 and let d=5

To find the horizontal asymptote;

We take the limit as x approaches infinity, we will get

thus we will take the derivative of both the top and bottom but L'hopital rule

If we look closely at the graph above we see that the vertical asymptote is similar to when changing in c.

This is what values will not work in the range, given our domain. We know our domain is going to be .

So which values will make our equation explode?

That is when the denominator equals 0. This will happen in every graph when

Negative Investigation

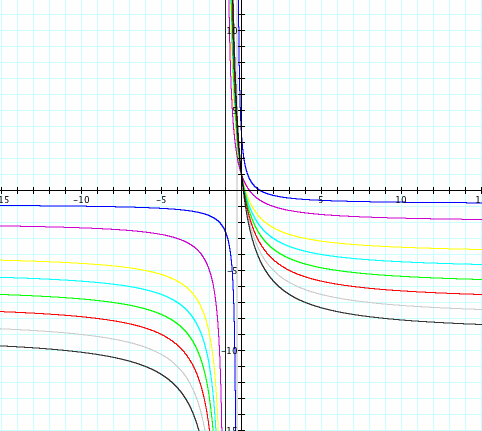
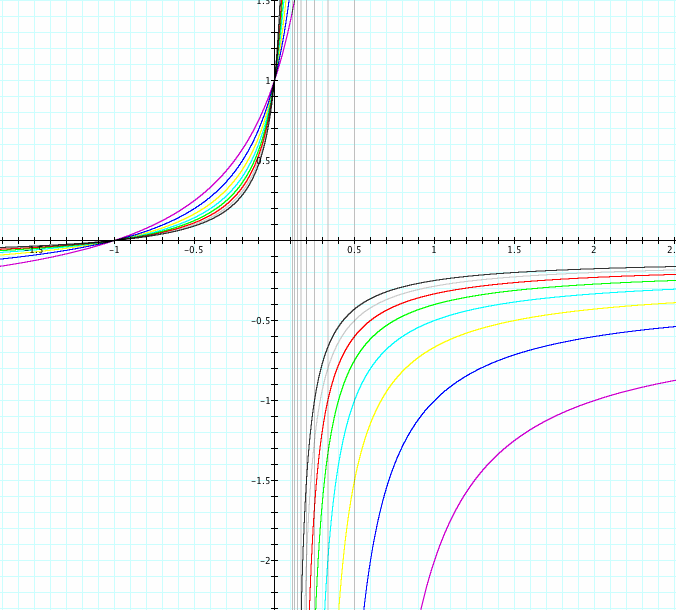
Here I have placed the graphs for the when we change a,b,c, and d to values (-2,-9). To find the values from that above such as asymptote we can do similar cases for all.

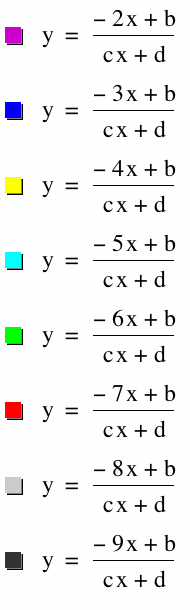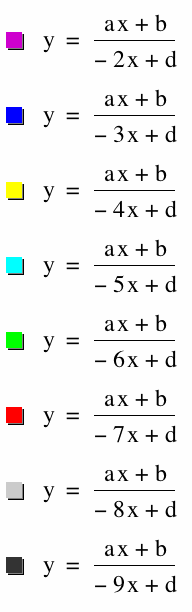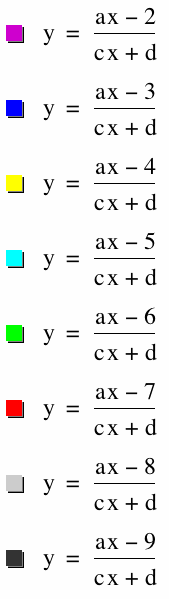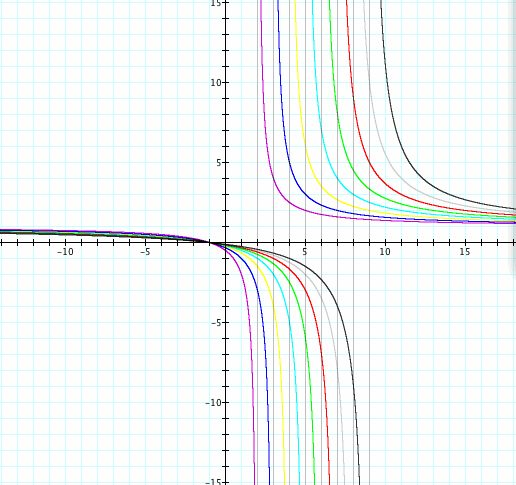Since 1 and 0 like to be difficult I decided to place them in a group of their own.

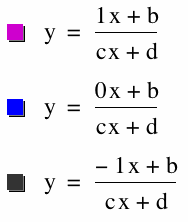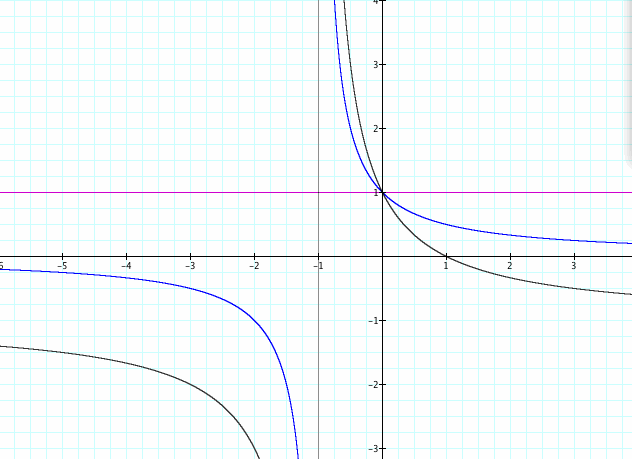Above we have let -1<a<1 to see what will happen.

If we let a=1

Domain will be and our range will be 1

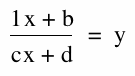or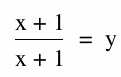

Thus we get the line y=1.

If a= 0.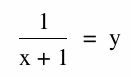

We notice right away that we are going to have a vertical asymptote as -1.

For horizontal we let x approach infinity and see we have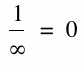

If we let a=-1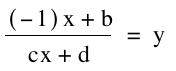or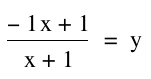

Again we notice immediately that there is a vertical asymptote at x= -1

However we have a shift in our horizontal asymptote.

Let x approach infinity. Thus we get 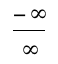So by L'hopital's Rules we will get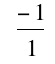

Or a horizontal asymptote of x=-1

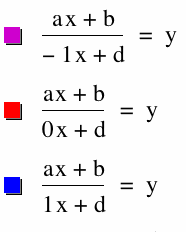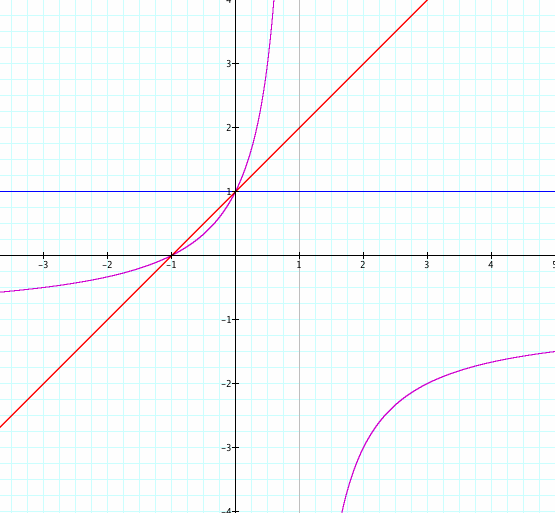Look at the red graph we have a nice line at . Thus no horizontal of vertical asymptotes, we have both domain and range

If c is to equal 1 we get 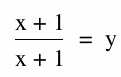Thus a horizontal line y=1

Let c= -1 then we have some changes.

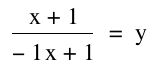
We notice that we are going to have a vertical asymptote at x=-1.

When we let x approach infinity we get The we have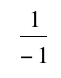

Our horizontal asymptote is at x=-1

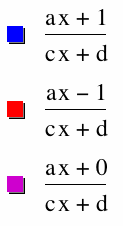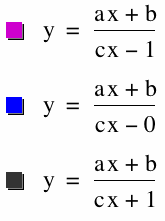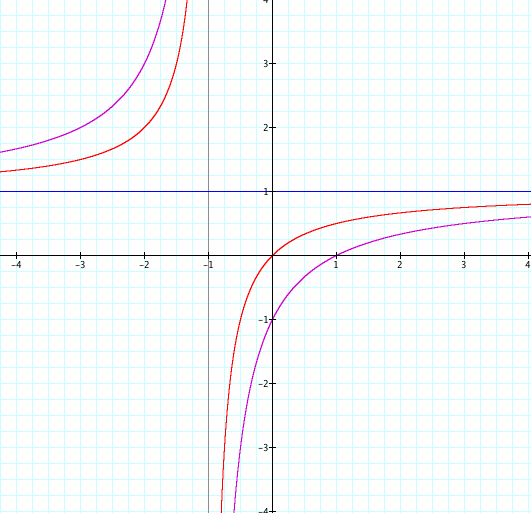
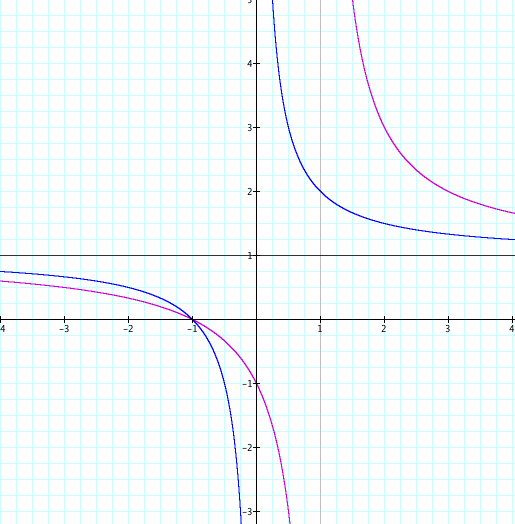Looking at the graphs about we notice that have many tings in common. One being the horizontal asymptote. This is because both limits will be 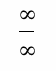thus x=1 by both after applying L'hopital's Rule.

another similar idea is that when b,d=1 there is a line at y=1.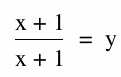

WE can see that on the left graph when c=-1,0 we will have a will have a vertical asymptote at x=-1. this is because we will always get the denominator and when we set this equal to zero we get

Thus a vertical asymptote.

For the graph on the right we have two, x=0, x=1. The blue is from having just x in the denominator of ratio, and the other from x-1 in the denominator will create x=1.

Home

E-mail me