

Ronald Aguilar
Barney is in the triangular room. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point?
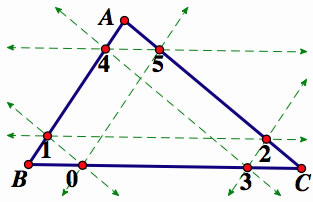
We have numbered the times Barney hits the wall by the intersection on each wall. From the directions, Barney has to take a path that is the parallel with the opposite side. Since the first 3 intersections(at the wall) are given, once we get to intersection number 4, we take a parallel with BC and move from that point. Once we get to number 5, we take a path that is parallel to AB. As you can see, Barney hits the wall 5 times prior to returning to his original position.
We constructed the paths with parallels. This enables us to draw on some theorems and make some proofs.
The parallels produced similar triangles (shaded in with color) and parallelograms.
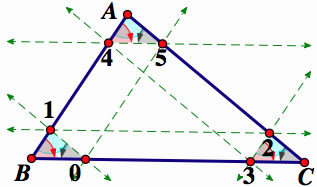
Using AIA(Alternate interior angle) Theorem which states that the pairs of angles on opposite sides of the transversal but inside the two lines are alternate interior angles. If the two line being crossed are parallel lines, then the alternate interior angles are equal.
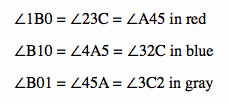
Based on what we know about parallelograms B0 = 45.
According to ASA(angle side angle postulate), two angles and the other included side of one triangle are congruent to two angles and the included side of another triangle, then these two triangles are congruent.
Since ![]() ,
,
the two triangles 1B0 and A45 are equal.
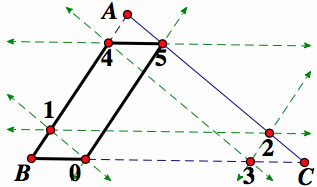
Parallelogram B321 makes B1 = 32 so from ASA, triangle B10 = triangle 32C. Triangle B10 = triangle 32C = 4A5.
Angle AB0 and angle ABC are connected to the same angle. Also, angle ACB and angle 23C have the same angle.
Since these angle share the same angle by the Angle Angle postulate the bigger triangle ABC is similar to the 3 smaller triangles: 1B0, 23C, and A45.
Now, lets check the path that Barney took to show he started at the same point and returned to that exact same point.
Parallelogram 0C21 makes 01 = C2. We proved these angles earlier:
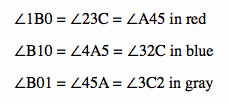
So Triangle B10 is congruent to triangle 32C.
Parallelogram 3C54 makes 3C = 45. From congruent triangles B0 = 3C and B0 = 45 which we confirmed earlier.
We have a caveat:
Parallelogram 0B45 makes 45 = B0. So, 45 = B0 ---> B0 = B0. 0 = 0.
Why is this important?
It shows that starting and ending point for Barney are the same.
Now, we have to verify the distance Barney traveled. We need to make this algebra easier so lets substitute variables for the sides.
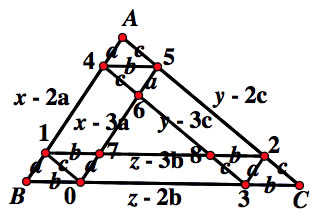
B1 = 4A = 65 = 07 = 32 = a , B0 = 17 = 82 = 3C = 45 = b , 10 = 46 = 83 = 2C = A5 = c
We need to account for the big triangle sides: AB = x , AC = y , BC = z
03 = z - 2b , 52 = y - 2c , 41 = x - 2a.
*We aware not to confuse the sides with the algebraic numbers(Sides in plain text, algebraic equations in bold and italic)*
We have to account for the segments 67, 78, 86.
Parallelograms 1038 makes 03 = 18. 03 = z - 2b. 78 = i.
z - 2b = b + i , z - 3b = i = 78
So, 76 = x - 3a and 86 = y - 3c.
c + { b + ( z - 3b) + b } + a + { c + ( y - 3c) + c } + b + { a + (x - 3a) + a } =
c + 2b + z - 3b + a + 2c + y - 3c + b + 2a + x - 3a = x + y + z
What does this equation remind us of ??? The perimeter of a triangle is its sides added together. AB + BC + AC = x + y + z.
This is the distance Barney traveled.
What happens if Barney starts at the midpoint of the triangle?
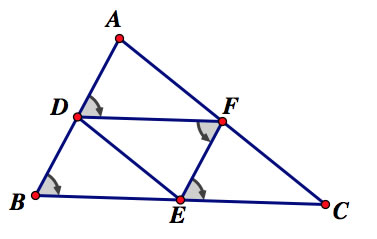

This time lets start from the orthocenter which is inside the triangle here...
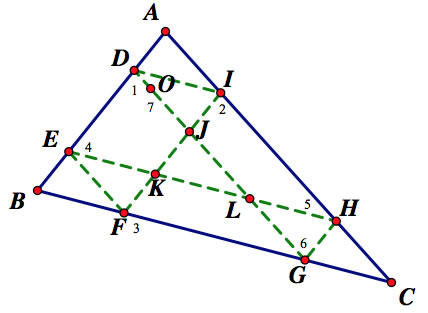
As you can, Barney hits the wall 6 times before returning to the othocenter.
BF = GC = DI = a , BE = DA = HG = b , EF = AI = HC = c
We account for the path OD to eventually JO so JO = p and OD = c - p
IH = x - 2a , ED = y - 2b , FG = z - 2c
KJ = y - 3b , JL = x - 3a , KL = z - 3c
Add everything together we get:
(c-p) + a + b + y - 3b + b + c - 3a + a + b + c + x - 3c + p = a + b + c
Again, the path equals the perimeter of the triangle.