Extra Write Up

Ronald Aguilar

I pulled the assignment from Assignment 1, problem number . Here, we will graph the function

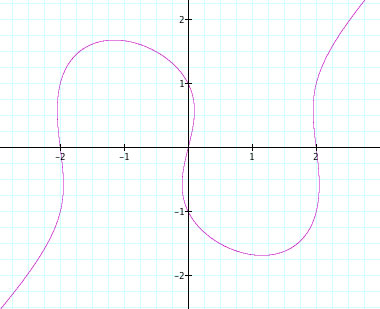
First, notice the shape of this graph. Second, take into account the number 4 in the left side of the equation and the number 1 in the right side of the equation.

Now, lets alter the value, where 4 is, on the left side of the equation and see what happens.

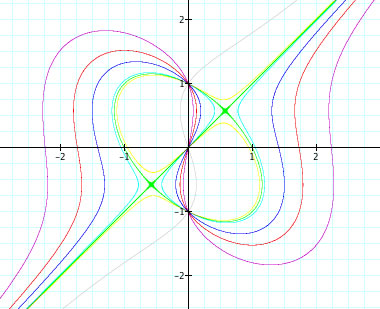
Here are the functions for each graph:

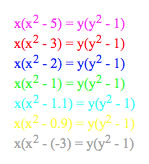
If we look at the initial graph of , we can see that the function intersects the graph at x = -2, 2. Also, the graph interects the graph at y = -1,1.

There are different variations of the functions, changing based solely on the variable x. Notice how all graphs y values stay the same, but change based on x. The function focuses on the changes in value x. Those values are affected by n = 5, 3, 2, 1 ,1.1, 0.9, and -3.

All the graphs intersect at y = -1,1. We understand this to be because of the right side of the equation, .

Once the functions values, inside the parentheses, get closer to each other, the graphs want to intersect each other. Finally, when they do intersect at , they create two points of intersection.

Also, the graph with n = -3, in the equation , seems to mimic the graph with n = 3. However, the symmetry with the origin is not present because of the additive property.

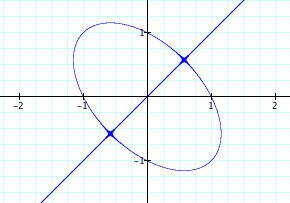
Lets see what happens when we graph   and independently of one another.

  in blue

in red