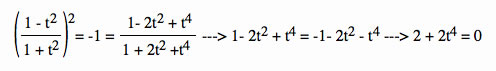Ronald Aguilar
Mathematically, parametric equations is a method of defining a relation using parameters. A parametric equation defines a relation as a set of equations.
Using the equation for a parabola 
, we can parametrize it using
x = t, 
. So, using the equation for a unit circle 
, we parametrize it with 
. So, x = cos(t) and y = sin(t).
Lets plug in some numbers and use and plug in some numbers to see how we come to understand the graph.
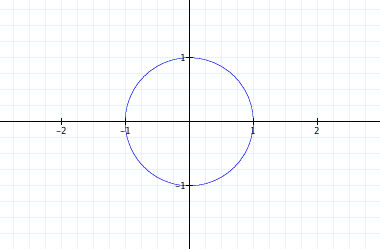
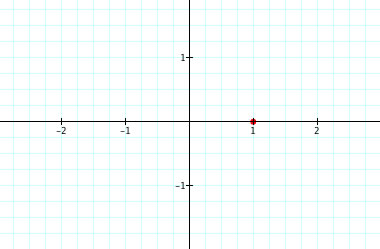
If t = 0 ----> x = cos(0) = 1, y = sin(0) = 0. This gives us the point (1,0) from (cos(0), sin(0)). If we increase from 0 until we get to 
, we will form a complete unit circle. Here is a better look at the parameters:
How?
Lets move along and now consider the equations:
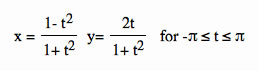
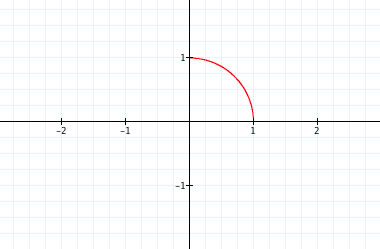
This is the graph without the interval.
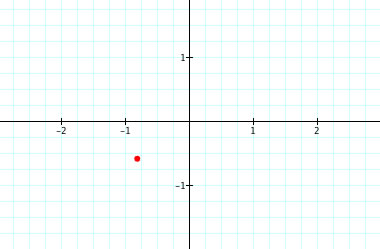
This is the graph with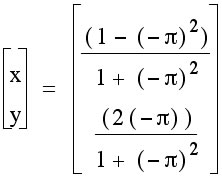 
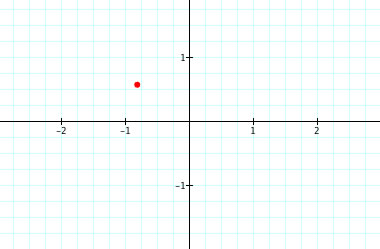
This is the graph with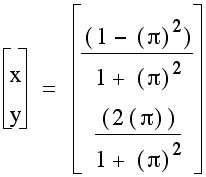 
.
This is the graph with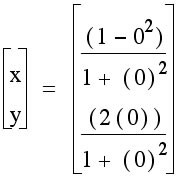 
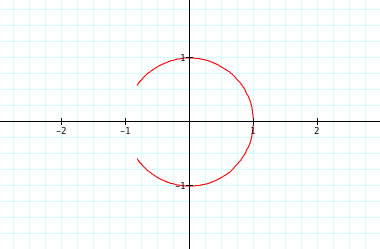
This is the graph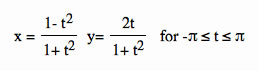. We can clearly see that from the first three graphs that we needed to trace and plot every point on the range. The first three graphs gave us an idea of how this graph would react with those three points plotted.
The graph is obvious circular due to the points lying on the unit circle but look using math:
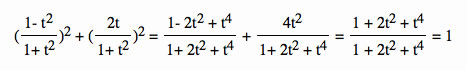
There is one problem that we can see with this graph. It does not complete the entire unit circle. There is a gap obviously because the points are not plotted. Let see why.
Lets first take a look at the original equations .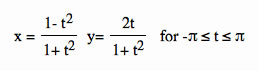
Notice that in the equations t is always squared so there is no way x can equal -1. The reason that x = -1 is important, if you look at the graph we need that point to complete the unit circle.
Lets do some math to prove this...
