Quadratic and Cubic Equations

Ronald Aguilar

Considering graphs in the xc planes using

Lets start by using different coefficients for a

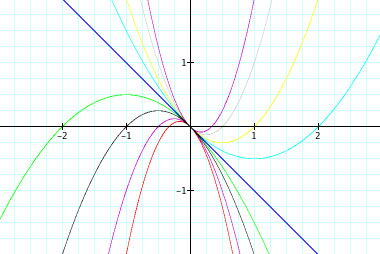
in black

in purple, bottom graph

in red

in blue

in green

in turquise

in yellow

in gray

in purple, top graph

Now, lets use different coefficients for b

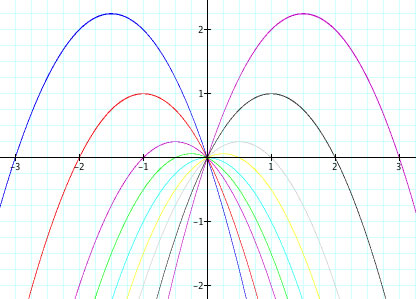
in purple, bottom graph

in red

in blue

in green

in turquise

in yellow

in gray

in black

in purple, top graph

As you can see, no matter what the vertices are the parabolas all go through the origin (0,0) and intersect one another. To get a general idea of why this is, I looked at each equation and of course noticed that every equation has . If we were to solve for y, we simply substract y from both sides of the equation. I concluded thats why all the parabolas showed negative characteristics for parabolas. All the parabolas have a maximum point. Lets graph the equation to see what happens to the intersections of the graph.

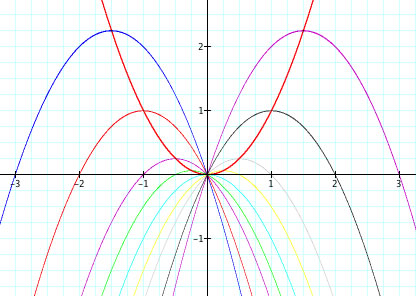
The parabola goes through every vertices. Lets use the original quadratic equation . In order to get the vertices of this equation and any other equation we must complete the square. In all this is expressed into vertex form:

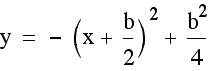
If we go back through and complete the square for each equation we get the vertices to be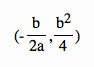

Where the axis of symmetry is x =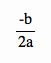. If we were to "fold" the parabola in half this where we "fold" the parabola.

In summary, notice that y-coordinate is the square of the x-coordinate. That is why the vertices touch the parabola .

, (h,k) is the vertex.