

by Ronald Aguilar
The median of a triangle is a segment whose endpoints are a vertex of the triangle and the midpoint of the opposite side.
Centroids of the triangle is the concurrency of three medians of the triangle. Concurrency means the three lines intersect at a certain point.
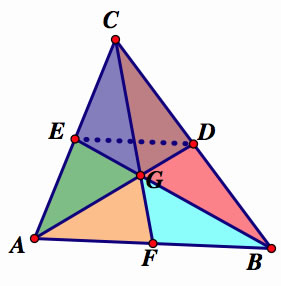
E is the midpint of segment AC and D is the midpoint of BC. DE is drawn so it can represent the midsegment of the bigger triangle ABC. This is parallel to the base. The segment DE is equal to half of AB.
There is an hour glass shape of two similar triangles. Triangle ABG is similar to EGD.
How do we know this?
Using the alternate interior theorem which states that the pair of angles on opposite sides of the transversal but inside the lines. DE and AB are parallel lines. We can use AD or BE as an transversal. Therefore, making angle DEG and angle GBA congruent. Also, angle EDG and BAG are congruent. Now, both triangles have two similar triangles. We now know that these are similar triangles.
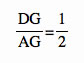
Since we now have this ratio, we can use it to solve for the proof. DG is basically one part and AG is two parts of the same part. If we split AG into 2 parts we get DG. So, the entire segment of AD is now cut into thirds or three equal parts.
If we follow the same logic we get  and
and 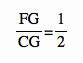 .
.
The centroid G is now ![]() distance from the vertex A, B, and C to the opposite side.
distance from the vertex A, B, and C to the opposite side.
Prove that medians divide a triangle into six equal triangles. Show these triangles all have the same area.
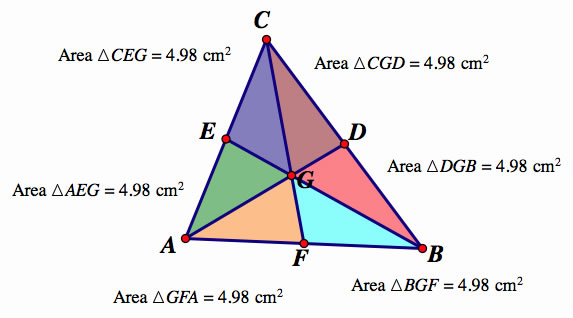
To start, two triangles with the same altitude have different bases, ratio of their areas is just the ratio of their bases.
Why is this important?
Next, lets show that triangle ACF is half of ACB. Coming from C, the two triangles share the same altitude (CH denotes the altitude in the graph below). Like we just stated, the ratio of their areas is the ratio of their bases AF and AB.
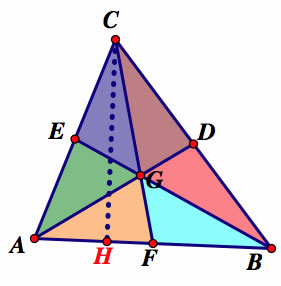
F is the midpoint of AB. AF=AB. Triangle GAF is a third of triangle CAF .Triangles GA Fand CAF have the same altitude from A. Ratio of areas is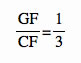 . Remember that
. Remember that 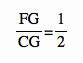 from proving the distance from the vertex to midpoint of opposite side is the centroid. This is important because it proves that
from proving the distance from the vertex to midpoint of opposite side is the centroid. This is important because it proves that 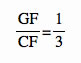 . We have
. We have

We can do this for the other 5 triangles to prove six triangles of equal area. The triangles are not congruent but have equal area. Establishing the rule of having the same base and altitude, equals the same area, helped us draw this conclusion.