Ronald Aguilar
Problem 2
Using three line segments that are medians of a triangle, lets constuct this triangle and show that it is unique.
It can be easy to construct the medians of a triangle but it be difficult to produce the triangle using the medians.
We know that medians cut at a ratio of 2:1. From assignment 4, we know that centroid is 2/3 the distance from a vertex to the midpoint of that opposite side. Therefore, the ratios formed from the triangle ABC:
CG : GF = AG : GD = BG : GE = 2 : 1
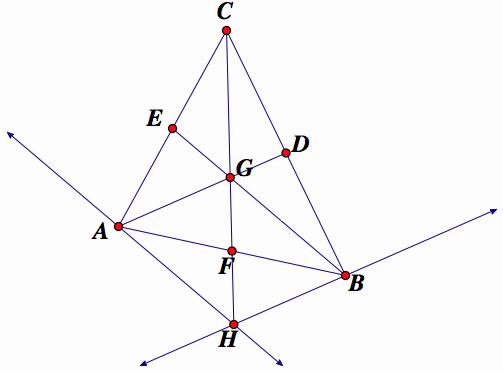
Using GSP we produced the triangle ABC, producing medians at AD, BE, and CF.
Construct a parallel to GB going through A, creating AH.
Construct a parallel to AG going through B, creating BH. We have produce a parallelogram AHBG. So, GF=FH, AF=BF.
Since CG : GF = 2 : 1, we know that GH = CG.
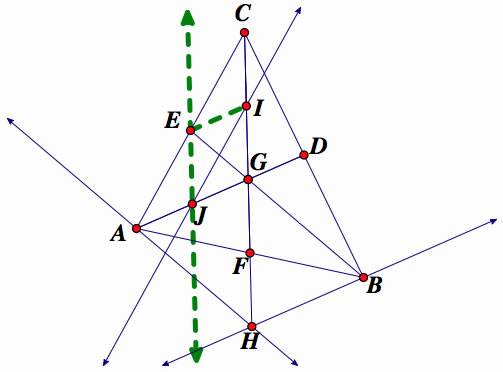
If we reflect GF on G to find the midpoint of CG, we get GI.
IConstruct a parallel to CE running through I, we get J. Also, if we construct a parallel to GI running through E we get EJ.
Using the same logic as early by creating this parallelogram EJGI we know EI=GJ. J is the midpoint of AG. GJ=EI which is a third of AD.
So we have CE=AE. We can produce BG by EG since EG is a third of BE.
Problem 2
Using three line segments that are medians of a triangle, lets constuct this triangle and show that it is unique.
* Here we are using the midpoints to construct its triangle. Not constructing the triangle using its midpoints. *
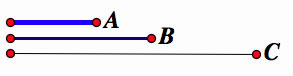
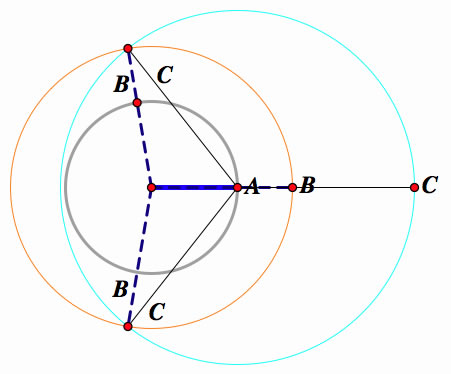
A) Referring to the graph below, construct a circle like the gray circle below using line segment A.
B) Next, construct a circle like the orange circle below using the line segment B, coming from the same center as A.
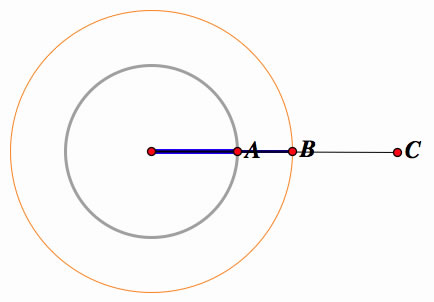
C) Use the line segment C, coming from the center A, to construct a third circle that intersects the second circle.
D) There should be two intesections formed from the second and third circles intersecting.
E) Connect the line segment (radius) B for the orangle circle to the intersection of the blue and orangle circle, on top and bottom.
F) Finally, connect the line segment (radius) C for the blue circle to the intersection of the orange and blue circle.
G) We have successfully constructed a triangle that is unique!