

Ronald Aguilar
Given two circles and a point on one of the circles. Construct a circle tangent to the circles with one point of tangency being the designed point.
Here in the construction of the figure that we need to solve the our problem. There is circle with center A. The circle inside with center B and a point C on circle A.
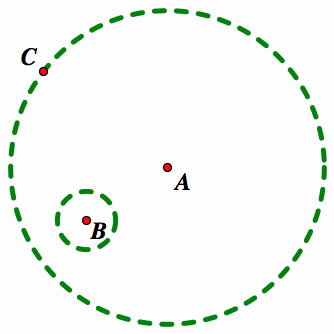
The problem gives two different solutions.
Why?
The circle can run through the point C with a distances closest to C on circle B, with the circle B outside of the tangent circle. Center D displays this below.
Also, The circle can run through point C with a distance farthest to C on circle B, with the Circle B inside of the tangent circle. Center D' displays this below.
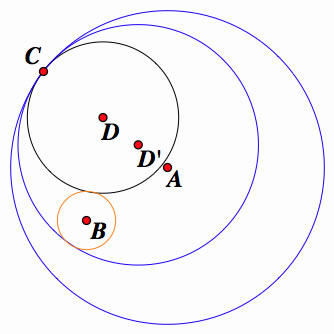
A) We construct a line to go through the center A and point C.
B) Using the center C, we construct a circle. Use the radius from center B.
C1) For the 1st graph - Using the new circle C (outside circle A) we created, make a point E at the intersection of the circle and line through E.
C2) For the 2nd graph - using the the new circle C (inside circle A and circle D') we created, make a point E at the intersection of the circle and the line through E.
D) Construct a segment (pink) between E and B. The gray line is constructed as a perpendicular line to F and segment EB.
E) The center D' intersects the gray line and blue line.
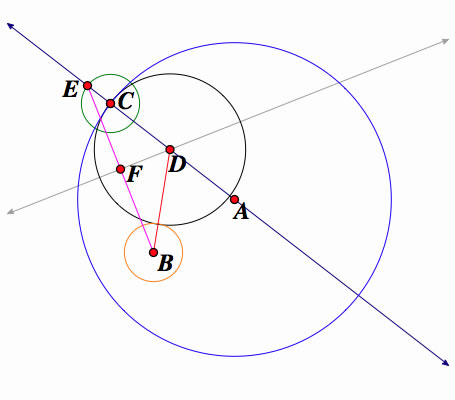
Circle B outside tangent circle D
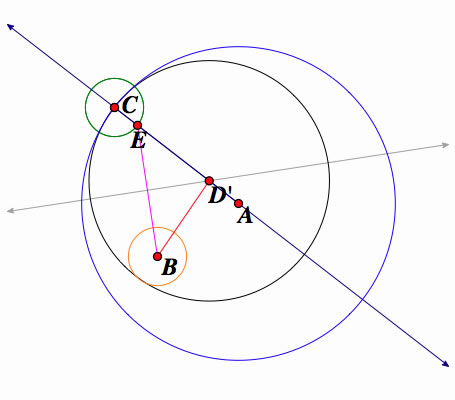
Circle B inside tangent circle D'
Moving C about the circle A. Center D will make an ellipse.