

Ronald Aguilar
The internal angle bisectors of triangle ABC are extended to meet the circumcircle at points L, M, and N, respectively. Find the angles of triangle LMN in terms of the angles A, B, and C.
The triangle ABC is formed. We construct the midpoints of AB, BC, and AC. The midpoints respectively are D (for AB), E (for BC), and F (for AC).
Now, lets construct perpedicular bisectors through the midpoints D, E, and F. These constructions form the circumcenter at point G.
The circumcircle is in green, by using the circumcenter G, going through the points A, B, and C.
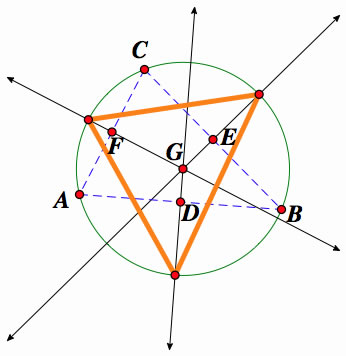
By creating the angle bisectors (in red dotted lines) for A, B, and C we get the following picture...
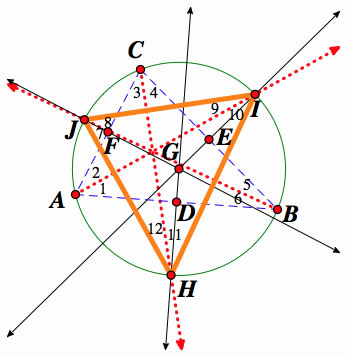
Finally, the problem asks us to find the angles of LMN in terms of ABC's angles.
∠3 = ∠10 because an inscribed angle is half the corresponding central angle. All inscribed angles that subtend the same arc are equal, so ∠1 = ∠8, ∠2 = ∠11, ∠12 = ∠5, ∠6 = ∠9, and ∠7 = ∠4.
∠A = ∠8 + ∠11 ∠B = ∠12 + ∠9, ∠C = ∠10 + ∠7, ∠H = 11 + ∠12, ∠I = ∠9 + ∠10, ∠J = ∠7 + ∠8, so ∠H = (1/2)A + (1/2)B, ∠I = (1/2)B + (1/2)C, and ∠J = (1/2)A + (1/2)C.