

By Ronald Aguilar
The pedal triangle is constructed with respect to the triangle ABC, below, with point D being inside the pedal triangle EFG.
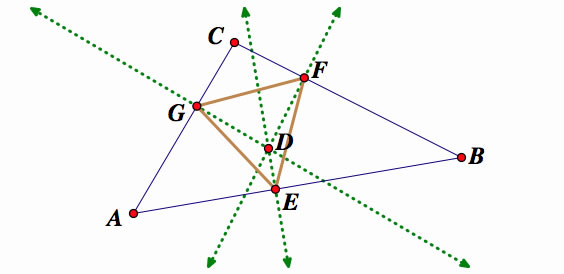
How did we form the pedal triangle EFG?
Triangle ABC is formed with point D placed inside the triangle.
Take point D and make perpendicular lines through D and through each side.
The points that are formed are E, F, and G. These are called the feet of the pedal triangle.
Connect the points E, F, and G with line segments and this is your pedal triangle.
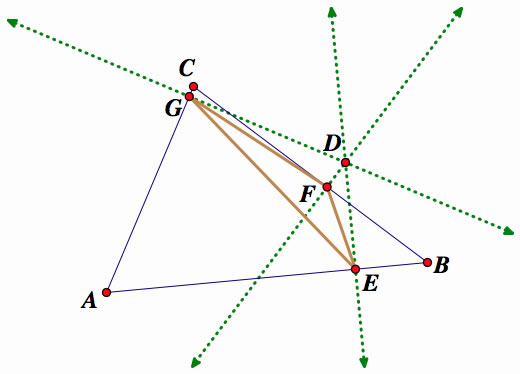
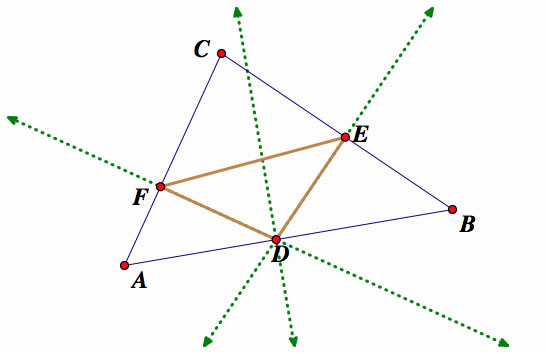
The pedal triangle is constructed with respect to the triangle ABC, below, with point D being outside the pedal triangle EFG.
Using the same logic as before we construct the pedal triangle.
What happens if the pedal point D is on the side of triangle?
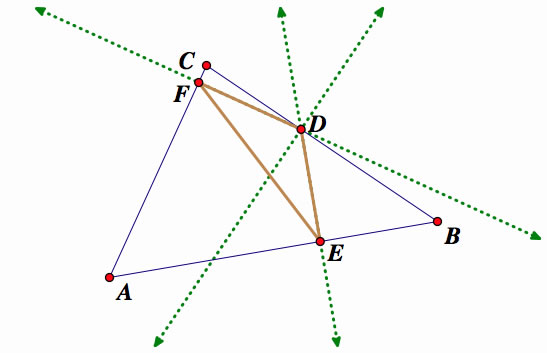
We can clearly see that the pedal point D is a vertex of the pedal triangle.
This happens no matter what side the pedal point D is placed on.
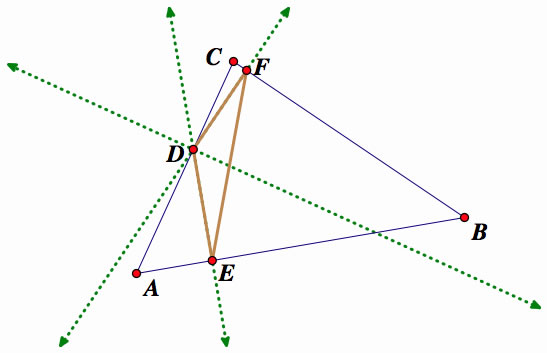
Also, the pedal point D constructs an obtuse triangle always, as previously shown on the last three graphs.
Also, notice how the perpendicular lines have turned into sides of the pedal triangle. The pedal point has became a vertex of the pedal triangle.
Why?
The pedal triangle is dependent upon its location. Why a pedal triangle? A bike's location is dependent upon the pedal of bike. So, the pedal points location is important.
What happens if the pedal point is one of the vertices of triangle ABC?
Lets make point A the pedal point on the triangle ABC. Slide point D onto the vertex A to make D a vertex.

As you see, there is not a pedal triangle anymore. The triangle has collapsed. The side DF collapses into the vertex A and now, vertex D which is the pedal point. The point F of the pedal triangle collapses into the vertex A and now, vertex D which is the pedal point. This makes EF collapse onto DE. If we look at the graph above this is demonstrated. DE is the only segment left. No angles can be accounted for. They are either undefined or zero.