Polar Equations

Allyson Faircloth

For this investigation, we will be looking at . We will see how varying a and b changes the graph. 

First let's look at .

We can see that we get the "n-leaf rose" shape. We also have y-intercepts of 1 and -1.

Let's look at different values for a and b.

         

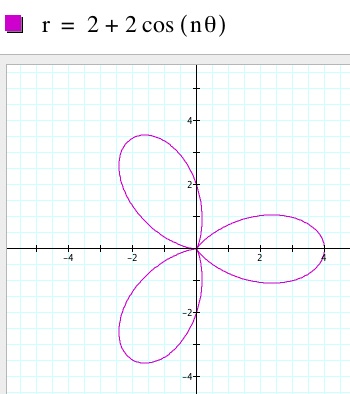
We can see that when a and b are both 2 we now have larger petals and y-intercepts of 2 and -2.  Then when a and b are both 20 we have even larger petals with y-intercepts of 20 and -20. We can conclude that the larger the values are for a and b, the larger the petals of our "n-leaf rose" will be.  Also, we will have y-intercepts at n and -n.  Below is an image of all three pictures together. 

Now let's take a look at a when n is varying. 

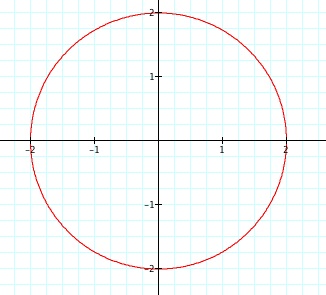
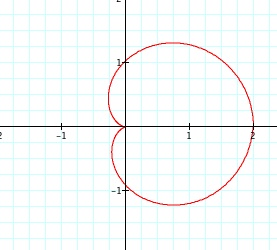
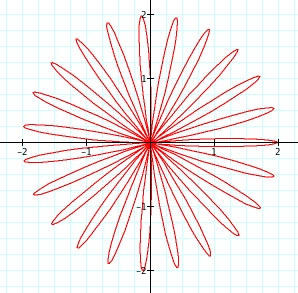
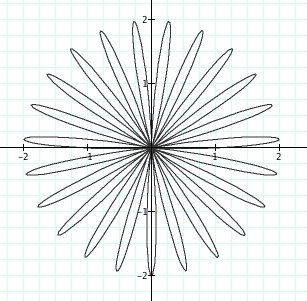
If we look at the animation above at specific times, we can notice some interesting things.  First of all, when n = 0, we just get a circle.  Then when n = 1, we get an odd shaped petal.  Then an n gets larger, we notice that each time n changes we have n number of petals for our "n-leaf rose." We can even see that when n is not a whole number, we get partial petals. 

                n = 0                                    n = 1                                   n = 23                              n = 7.5

           

Another interesting aspect of varying n is for the time when 0 < n < 1.  For this interval we have a spiral because n has not yet reached 1, and therefore a whole petal has not been formed yet. 

n = 0.3

Lastly, let's look at what changes when we use sine instead of cosine. 

We see that we have very similar results. The variable n still relates to the number of petals we will have, yet those petals are not in the same spots.  They have been rotated ninety degrees counter-clockwise. 

               n = 0                                       n = 1                                   n = 23                                n = 7.5

              

 

 

Return