
Find The Parabola!
Allyson Faircloth
For this activity, we will be trying to find the equation of a parabola which is concave down and shares a vertex with the parabola 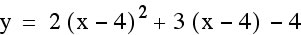 .
.
By looking at the equation 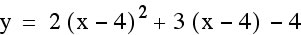 , we notice that there is a vertical shift down 4 units and a horizontal shift right 4 units from the more basic equation
, we notice that there is a vertical shift down 4 units and a horizontal shift right 4 units from the more basic equation 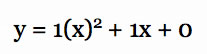 . Those are both isometries or translations. When 4 is subtracted from x, that is causing the horizontal shift or translations to the right 4 units. However if we add 4 to both sides of the equation, we get
. Those are both isometries or translations. When 4 is subtracted from x, that is causing the horizontal shift or translations to the right 4 units. However if we add 4 to both sides of the equation, we get 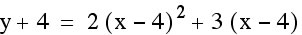 . The 4 being added to y is the vertical shift or translation down 4 units.
. The 4 being added to y is the vertical shift or translation down 4 units.
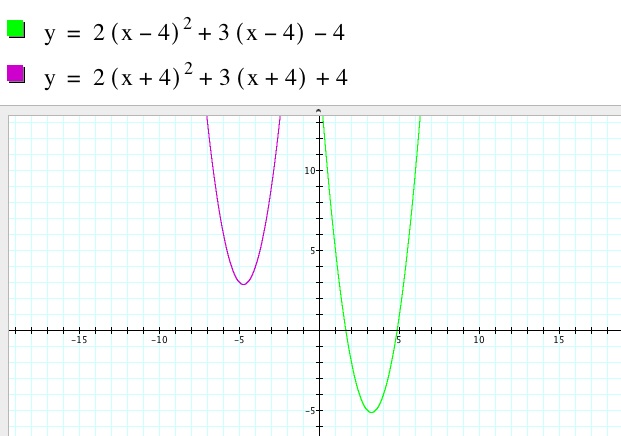
In order to transform the function into the second quadrant, we notice that we will need the translations of a horizontal shift to the left and a vertical shift up. The original equation had been shifted to the right and down. Therefore, if we change the signs of those shifts to positive then we should get a graph in the second quadrant. We have in fact used both vertical and horizontal translations to move the function into the second quadrant. We can see below that 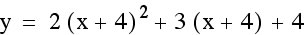 .
.
Now we need to change our function so that it is translated to the position that it has the same vertex as the last function (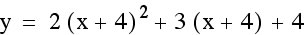 ) but is concave down. We know that a negative leading coefficient will make a function concave down so let’s try it.
) but is concave down. We know that a negative leading coefficient will make a function concave down so let’s try it.
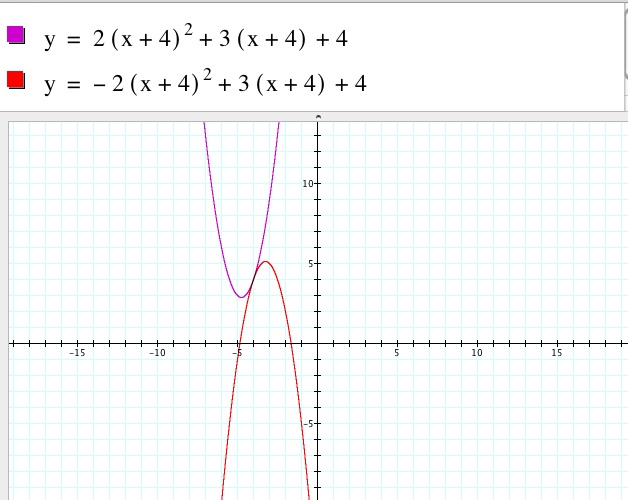
Making the leading coefficient negative made the function concave down, but the vertex has changed as well. Why did this happen? Let’s try simplifying our function so that we can more easily see how the positive translations are changing the functions.
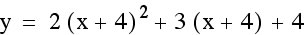
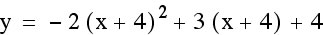
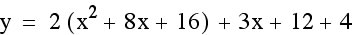
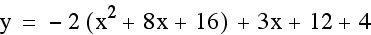
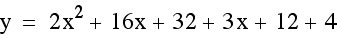
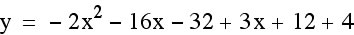
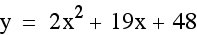
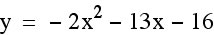
To find the vertex we must first find the x-coordinate by using 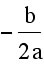 .
.
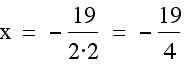
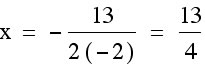
Now it is even easier to see that these two functions do not have the same vertex.
To check our x-coordinate for our function in the second quadrant, we can see if line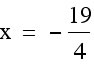 intersects our graph at the function.
intersects our graph at the function.
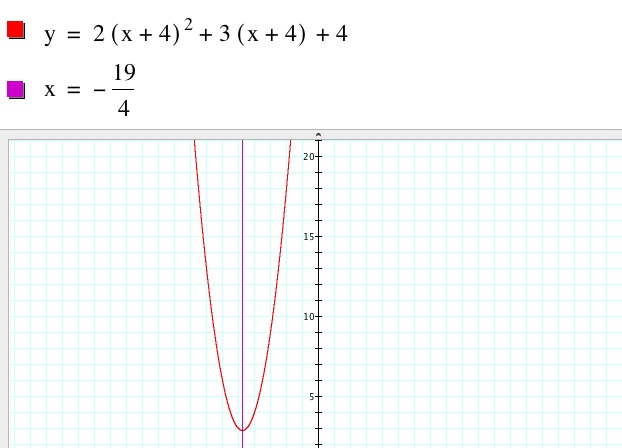
As we can see, the x-coordinate 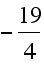 is correct, yet these two functions do not have the same vertex. However we saw from graphing the equation that we have the same graph concave but at a different vertex. Therefore, we can work from our simplified forms of the functions (
is correct, yet these two functions do not have the same vertex. However we saw from graphing the equation that we have the same graph concave but at a different vertex. Therefore, we can work from our simplified forms of the functions (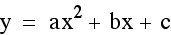 ). We will then be able to manipulate those functions to make the functions have the same vertex.
). We will then be able to manipulate those functions to make the functions have the same vertex.
First of all, we know our leading coefficient has to be a -2. So we can start with 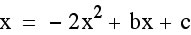 . We just need to find our b and c. Well we know that our x-coordinate only deals with a and b. We already have our b and that are x-coordinate has to be
. We just need to find our b and c. Well we know that our x-coordinate only deals with a and b. We already have our b and that are x-coordinate has to be 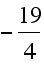 , so we can use that information to find b.
, so we can use that information to find b.
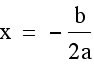

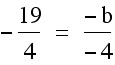
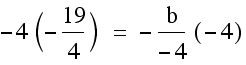
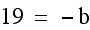
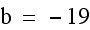
Now we have 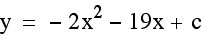 . We only need to find c. We need to know what our y-coordinate of our vertex is, so that we can use that value to find c. In order to find the y-coordinate of our vertex, we can plug in our x-coordinate for x into our equation and solve for y.
. We only need to find c. We need to know what our y-coordinate of our vertex is, so that we can use that value to find c. In order to find the y-coordinate of our vertex, we can plug in our x-coordinate for x into our equation and solve for y.
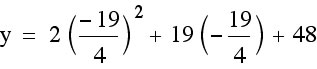
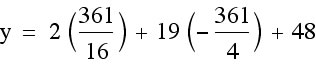
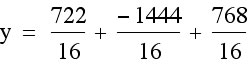
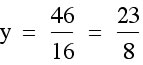
We can check our y-coordinate in the same way as we did with our x-coordinate. We can see if the line 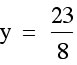 intersects our graph at the vertex.
intersects our graph at the vertex.
We can see from the graph that our y-coordinate is correct, so now we can use this y-coordinate to find c for our new function.
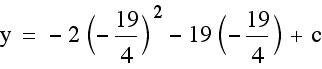
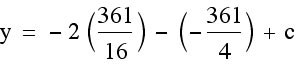
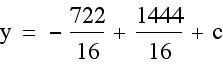
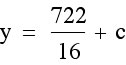
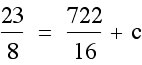
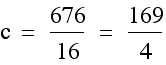
We now have all the parts for our new function.
Our concave down function with the same vertex will be 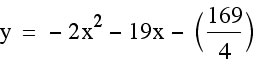 .
.
Let’s check our graph and see if our new function is correct.
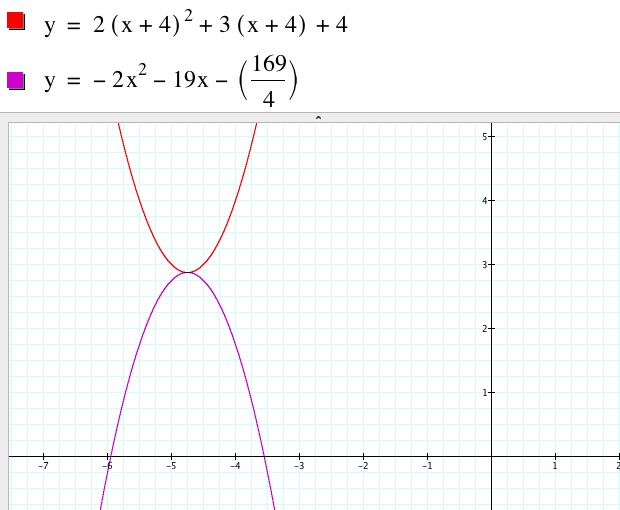
It appears that the two functions have the same vertex. Let's check with our vertical and horizontal lines for the two coordinates of the vertex.
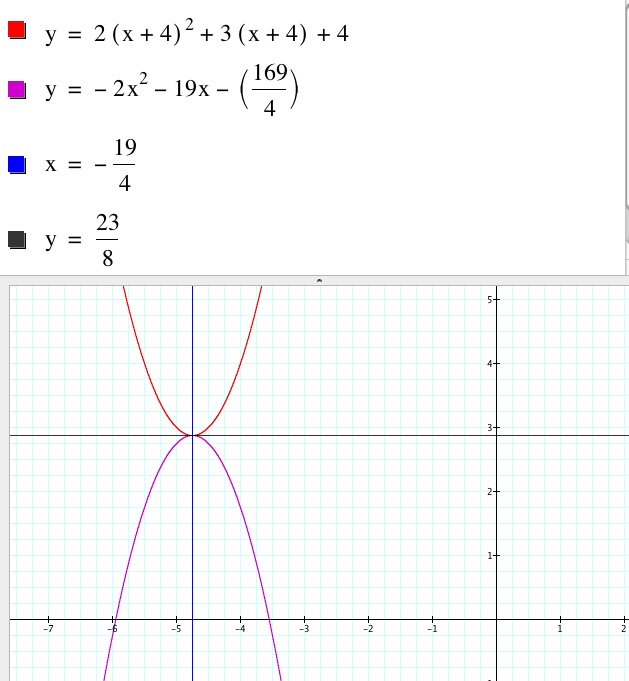
Indeed it is correct!
Now what can we generalize about this problem? First of all if we take a function and simply make the leading coefficient negative, the function is not going to have the same vertex if the function is not in standard form. Secondly, it is easier to deal with a function if you simplify the expression. Lastly, it is important to use information that we know about the original function along with our knowledge of translations and other isometries in order to correctly identify our new function.


.
, we notice that there is a vertical shift down 4 units and a horizontal shift right 4 units from the more basic equation
. Those are both isometries or translations. When 4 is subtracted from x, that is causing the horizontal shift or translations to the right 4 units. However if we add 4 to both sides of the equation, we get
. The 4 being added to y is the vertical shift or translation down 4 units.
.
) but is concave down. We know that a negative leading coefficient will make a function concave down so let’s try it.
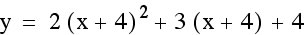
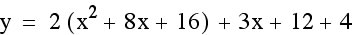
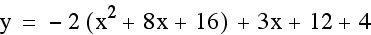
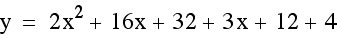
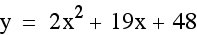
.
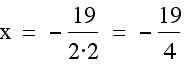
intersects our graph at the function.
is correct, yet these two functions do not have the same vertex. However we saw from graphing the equation that we have the same graph concave but at a different vertex. Therefore, we can work from our simplified forms of the functions (
). We will then be able to manipulate those functions to make the functions have the same vertex.
. We just need to find our b and c. Well we know that our x-coordinate only deals with a and b. We already have our b and that are x-coordinate has to be
, so we can use that information to find b.
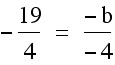
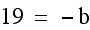
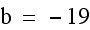
. We only need to find c. We need to know what our y-coordinate of our vertex is, so that we can use that value to find c. In order to find the y-coordinate of our vertex, we can plug in our x-coordinate for x into our equation and solve for y.
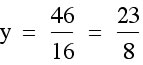
intersects our graph at the vertex.
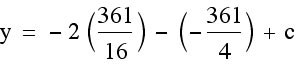
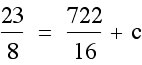
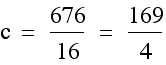
.