

You may or may not have heard of a town in Prussia known as Konigsberg. The people there had a very interesting activity which came to be a puzzle among them. The town had seven bridges which connected four pieces of land (See Figure 1 below). The task with which people challenged each other was to walk over every bridge in the town without crossing back over any bridge twice. You may wonder why this was such a challenge or may even think that it seems quite easy. Well then try it this GSP file!
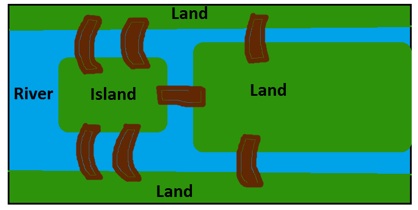
Figure 1
Teachers are encouraged to construct Figure 1 on the floor in their classroom such as in the picture below and allow students to try out some different paths.
Were you able to find a path??
The people of Konigsberg were unable to find a path as well. The famous mathematician Euler heard about the activity and traveled all the way to Konigsberg in order to prove that it could not be done.
We are going to use graph theory in order to prove that the Konigsberg Bridge problem is impossible. We will be using the graph from the GSP file above in which the land masses are vertices (points) and the bridges are edges (arcs).
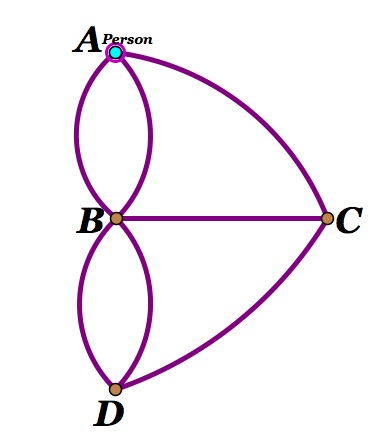
Proof:
1. We can see from the diagram above that vertices A, C, and D all have a degree of three (meaning they have three edges connected to them). Vertex B has a degree of five (meaning five edges are connected to B).
2. Now let's suppose that we start at one of the vertices that has a degree of 3. A person at this vertex could then move to either a vertex of degree 3 or a vertex of degree 5. So let's assume that we start at vertex A. If we start at that vertex we will have to leave that vertex, come back to the vertex, and leave that vertex again. (Figure 2 and 3)
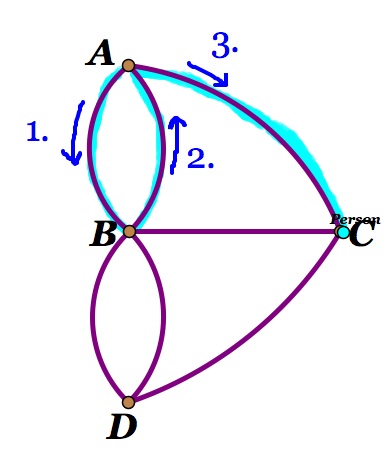
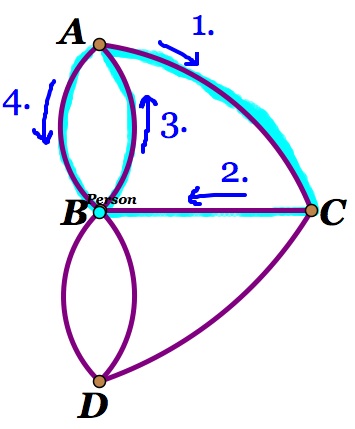
Figure 2 Figure 3
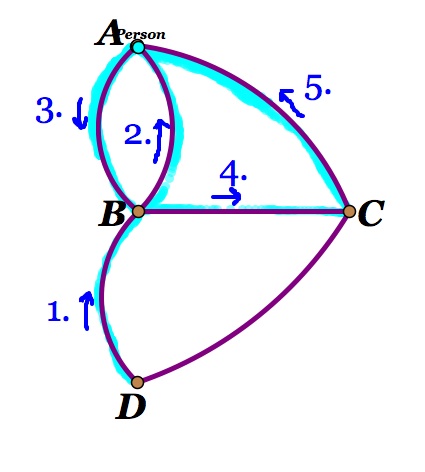
3. This creates a problem. When the person ends at C (Figure 2) you can see that now the person has two options. He can move to B or D.
Option A: If he moves to B then he will have to move to D. He then will only be able to move to B or C and not be able to get to the other bridge. (Figure 4).
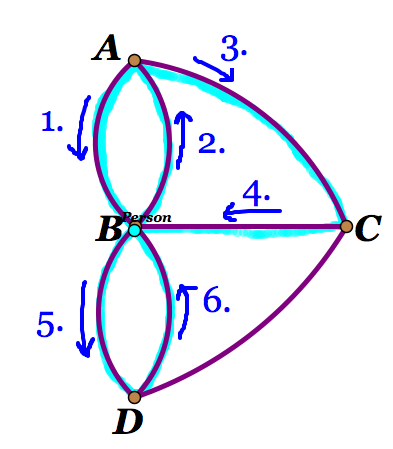
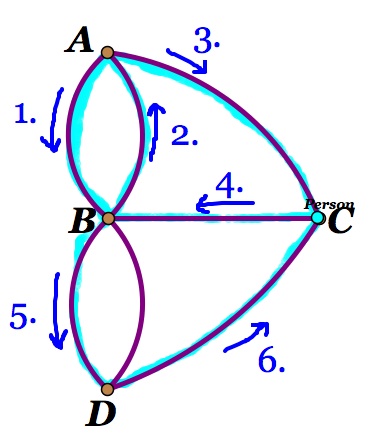
Figure 4
Option B: If he moves from C to D, then his next move will have to be to B which will leave him with the options of moving back to D or to C but still leaving him with one bridge left uncrossed (Figure 5).
Figure 5
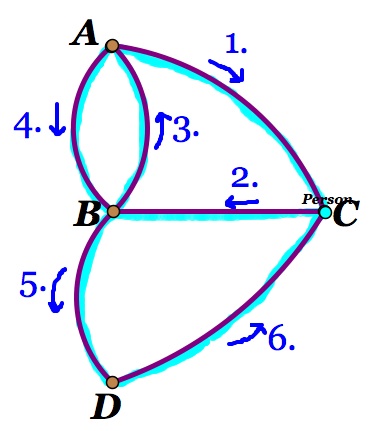
4. Let's look at Figure 3 when he ends up at B after the first three bridges. He now only has one option to go to D. But from D he is then stuck because if he goes back to B then he leaves off a bridge and if he goes to C he leaves off a bridge (Figure 6).
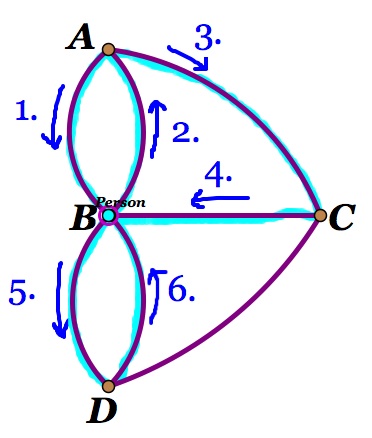

Figure 6
5. So we see that starting at a vertex of degree of three will not work. Let's try starting at vertex B which has degree 5. From vertex B we must then travel to a vertex of degree three. We then run into the same problems as we found by starting at a vertex of degree three. Figure 7 shows some examples of possible paths from B that leave one or either two bridges out.
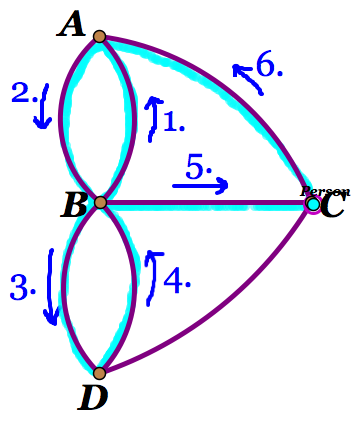
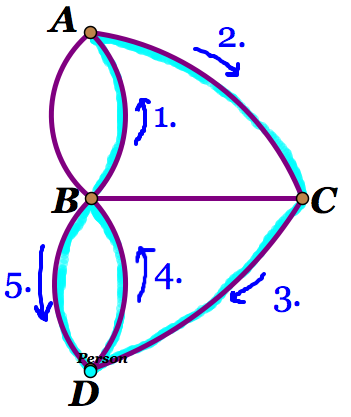
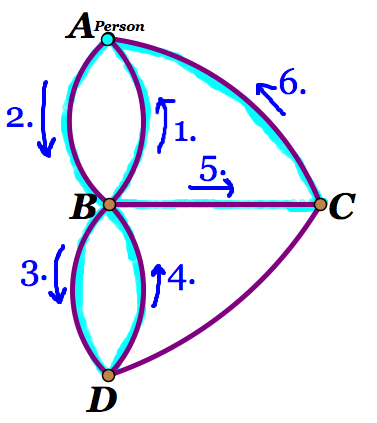
Figure 7
6. Therefore, the task is impossible without being able to swim across the rivers or use dynamite to get rid of a bridge. If a person starts at a vertex of degree three then they will have to leave that vertex, come back to it, and then leave it again. That will have used one of the edges going to another vertex of degree three. If you land on a vertex of degree three then you will have to leave that vertex and go back. That then leaves you stuck without being able to leave that vertex again when you still have another vertex of three that you must finish at as well. If you landed on the vertex of degree five then you would have used two of the edges going to the other vertex of degree three. You then would have to go back to that vertex leaving you stuck again!
Now try finding a path again but this time take away one of the bridges. You should be able to find a path now.
Let's consider first taking away one of the bridges which are going from land to the island (Figure 8).
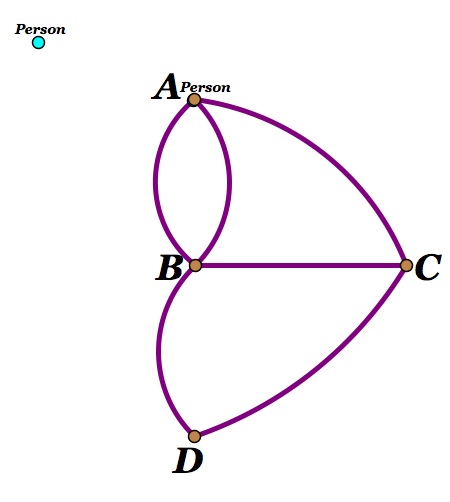
Figure 8
We now have two vertices (A and C) which have a degree of 3 and two vertices (B and D) which have a degree of 4 and 2 respectively. Let's first begin our path starting from a vertex of even degree. We will start at D.
As we can see this path leaves us with one bridge. Try different paths starting at D. You will find that those paths also leave one bridge without being crossed. We still can not find a path which will cross all of the bridges which are left. Let's try starting at a vertex of odd degree. We will start at vertex A.
We have found a path which crosses all of the bridges! Can you find another path?
So what does all of this tell us? We found that by taking away a bridge we were able to find a path which would cross all of the bridges once. However, we had to start at a vertex of odd degree. Let's see if we find the same results by taking away a different bridge.
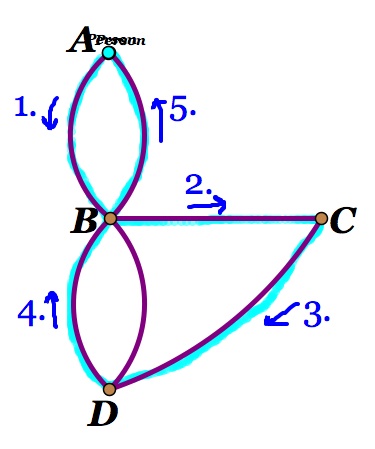
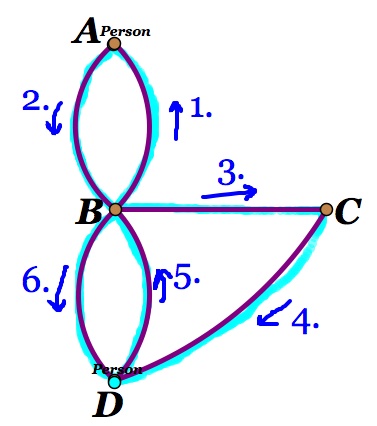
Figure 9 Figure 10
Figure 9 above shows a path starting at vertex A which has a degree of 2. We were left with one bridge unused. Figure 10 shows a path starting at vertex B which has a degree of 5. Once again we have found that by taking away one bridge we were able to find a path which used all of the bridges once if we started at a vertex of odd degree.
Why is it that starting at an odd degree didn't work unless we took away one of the bridges? Euler found from his trip to Konigsberg that in order to be able to find an 'Euler Path' (path which uses every edge once) from a graph there can be no more than two vertices of odd degree. Our original problem with all of the bridges contained four vertices which each had an odd degree. By taking away one of the bridges, we are left with two vertices of odd degree and two vertices of even degree.
For further investigation, try taking away different bridges or even adding bridges to the original problem to try to find other Euler paths.
Return