

Allyson Faircloth
This activity looks at all of the different paths Barney could take within a triangular room in order to get back to where he started. Barney can start anywhere he pleases; however, he can only move parallel to the sides of the triangles. Whenever he reaches a side of the room, he must stop and move parallel to a different side.
For this investigation, you will need to click here for a GSP file for Bouncing Barney. Different tabs from the GSP file will be used throughout this write-up. Before animating Barney for any of the tabs, make sure he has returned to the starting point by clicking "Move Barney to Start." Then in order to watch Barney move along the path click each "Move" animation button in chronological order. Each tab with animations will start Barney at a different location. We will make conjectures throughout the investigation and then prove that they are correct.
The first location we will look at is if Barney starts at a vertex. Find this tab in the GSP file. By starting at this location, Barney's path is the perimeter of triangle ABC. This is for the fact that if Barney is standing at a vertex then in order to walk parallel to a side he will have to walk on one of the two adjacent sides. If he had walked parallel to the opposite side, then he would have been walking outside of the room and would never meet another side. One possible path Barney could take would be A to B, B to C, C to A. This path only takes three moves.
Next, we will examine what happens if Barney starts outside the triangle. Find this tab in the GSP file. For this location we will need to extend the sides of the triangle. Here we can see that Barney's path is longer than the perimeter of the triangle, since the whole path is outside the triangle. Although once again he returns to his original position. This path requires six moves. If we had not started on one of the extensions, then the path would have taken seven moves. However, if we were to look at the direction in which Barney is traveling, we could say that one direction is a negative distance and the other is a positive distance. Then, we may find that the path Barney travels outside triangle ABC is in fact equal to the perimeter of triangle ABC. We can consider segment FG, HI and J(Start) to be negative distances. Then the perimeter of path (Start)FGHIJ - 2FG - 2HI - 2JC is equal to the perimeter of triangle ABC.
Now, lets start Barney on one of the sides. Find this tab in the GSP file. Here we see that Barney once again needs to move six times in order to return to his starting position. However, interestingly we find that the distance of the path is equal to the perimeter of triangle ABC.
We now need to prove that the above conjecture is indeed true.
Proof:
We want
AB + BC + CA = DE + EL + LH + HI + IL + LF + FG + GK + KD.
But AB = AD + DI + IB, BC = BH + HG + GC, and CA = CF + FE + EA.
So we get AD + DI + IB + BH + HG + GC + CF + FE + EA = DE + EL + LH + HI + IL +LF + FG + GK + KD.
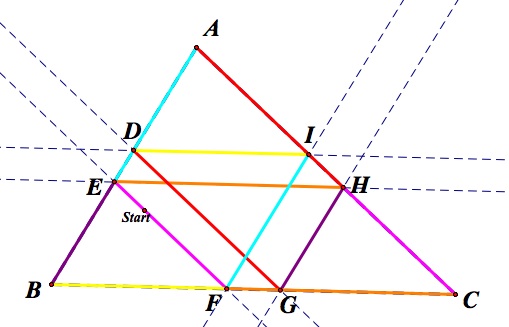
Since segment BD is parallel to segment HE and are intersected by the parallel transversals DE and BH, then DI is congruent to EL and DE is congruent to BH and IL. From this same reasoning along with the properties of parallel lines we find that angle ADE = angle IBH, andle AED = angle IHB. Then since AE = IH, then triangle AED is congruent to triangle IHB by SAS triangle congruency theorem. Therefore, AD = BI. Using the same reasoning as above, we discover the following congruencies (shown by same color on our image):
AE = IH = KG = FC,
BI = DA = HL = GF,
ID = LE,
LF = HC,
DK = EF,
and DE = IL = BH = GC.
So from the congruencies above, we get
HL + EL + FG +DE + LF + IL + IH + DK + GK = DE + EL + LH + HI + IL + LF + FG + GK + KD.
Therefore by the commutative property,
DE + EL + LH + HI + IL + LF + FG + GK + KD = DE + EL + LH + HI + IL + LF + FG + GK + KD.
Thus,
AB + BC + CA = DE + EL + LH + HI + IL + LF + FG + GK + KD.
So the distance of our path was indeed equal to the perimeter of the triangle.
Barney could also start at a specific point on a side. Let's start Barney at the midpoint of a side. From this tab of the GSP file, we can see that Barney must only move three times in order to reach his starting point again. This time the distance of the path is only half the perimeter of triangle ABC.
We now need to prove using similar and congruent triangles that the distance of that path is actually half of the perimeter of triangle ABC.
Proof:
First since DB and EF are parallel and the transversals DE and BF are parallel, then DB = EF and DE = BF. Also D, E, and F are the midpoints of the sides of the triangles. So BD = DA, BF = FC, CE = AE. We can then conclude BF = FC = DE and BD = DA = EF. Then by similar reasoning, DF = AE = EC.
The perimeter of triangle ABC = AD + DB + BF + FC + CE + EA.
But we know AD = DB, BF = FC, and CE = EA.
Therefore, the perimeter of triangle ABC = 2AD + 2BF + 2CE.
So from our previous congruencies we get the perimeter of triangle ABC = 2EF + 2DE + 2 DF.
Thus, the
perimeter of triangle ABC = EF + DE + DF which is the distance of Barney's path.
We could also start Barney at a point which at a point which marks the tri-section of a side of the triangle. Here we see that the path once again requires six moves to return to the starting point, and the distance of the path is equal to the perimeter of triangle ABC.
In order to prove that the distance of the path when Barney starts at a tri-section of a side is equal to the perimeter of the triangle, we can use the same reasoning as the proof for when Barey started on a side. The picture for that proof with congruent segment being the same color is below:
For the next part of the investigation, we will investigate Barney starting at a point inside triangle ABC. I have chosen an arbritrary point inside triangle ABC for the tab in the GSP file. I have also made two other tabs to examine Barney's paths if he starts at the centroid or at the orthocenter of triangle ABC.
Arbitrary Point Centroid Orthocenter
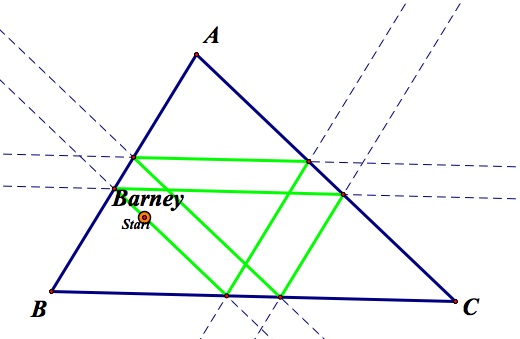
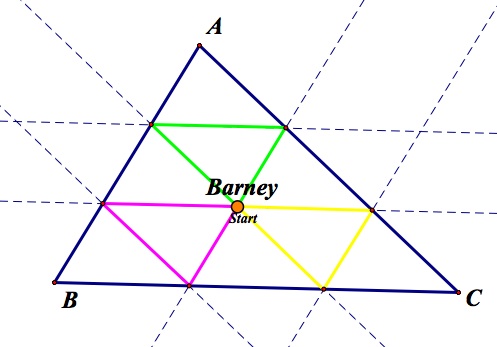
Interestingly for the arbitrary point and the orthocenter, the path takes seven moves to return back to where Barney started. This is because the starting point for both of these situation is on a segment between two sides. In order for Barney to travel the whole length of that segment, he must use two moves. That accounts for the seventh move. Also, both of these paths have a distance equal to the perimeter of the triangle.
We can use the same resoning as our proof for when Barney starts on a side of triangle ABC in order to prove the distance of the paths for starting at an arbitrary point inside the triangle and for starting at the orthocenter are equal to the perimeter of the triangle. The pictures below show congruent sides as the same colors.
Arbitrary Point Orthocenter
When Barney starts at the centroid of triangle ABC, we find some different characteristics than before. First of all, Barney has found the trisection points of each of the sides. Also, the distance of this path is equal to the perimeter of the triangle.
In order to prove that Barney's path from starting at the centroid is equal to the perimeter of triangle ABC, we will just look at the path from D to I, I to H, and H to D.
Proof:
The perimeter of triangle ABC = AI + IJ + JA + AE + EF + FC + CG + GH + HA.
But by properties of transversals with parallel lines, we know IH = FC = DG = EF = JD = AE.
By the same reasoning, JE = ID = AH = DF = HC = GC, and GF = DE = JA = IJ = HD = AI.
So the perimeter of triangle ABC = HD + HD + HD + IH + IH + IH + ID + ID + ID.
Then the perimeter of triangle ABC = 3HD + 3IH + 3ID.
Thus,
perimeter of triangle ABC = HD + IH + ID which is one of Barney's possible paths.
Therefore, the perimeter of triangle DGF and DEJ are also one-third the perimeter of triangle ABC. Thus, the total distance traveled by starting at the centroid is equal to the perimeter of triangle ABC.
Return