Parametric curves are pairs of functions of t such that one function of t sets an x coordinate and the other function of t sets the y coordinate. In this exploration, we will be looking at curves where x is a function of cos(t) and y is a function of sin(t). We will begin with the most basic pair:
x = cos(t); y = sin(t) for 0 
t 2
.
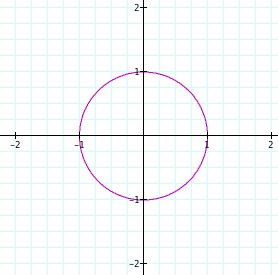
As you can see, this pair of equations gives us the unit circle. The fact that the unit circle can be written as this particular pair of parametric equations is the reason for all of the trigonometric implications of the unit circle.
Now, we will look at what happens when both functions are multiplied by a constant, giving us the following pair of equations:
x = acos(t); y = asin(t) for 0 t 2.
a = 2 in purple; a = 3 in red; a = 4 in blue.
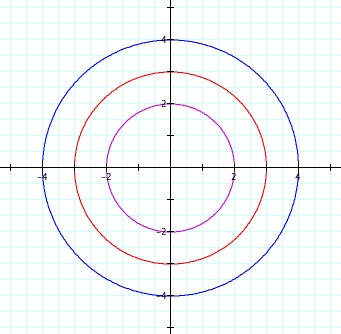
It is easy to see that when a 
0, this pair of equations gives us the circle centered at the origin with radius a. In the event that a is negative, the graph is simple reflected across the x-axis and the y-axis, giving us back the exact same graph. Therefore, this pair of equations gives us the circle centered at the origin with radius |a|.
Now, we will look at what happens when the first function is multiplied by one constant, and the second function is multiplied by a different constant, giving us the following pair of equations:
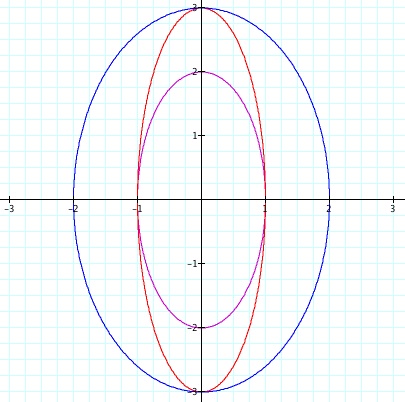
x = acos(t); y = bsin(t) for 0 t 2 and a 
b.
a = 1 and b = 2 in purple; a = 1 and b = 3 in red; a = 2 and b = 3 in blue.
a = 2 and b = 1 in purple; a = 3 and b = 1 in red; a = 3 and b = 2 in blue.
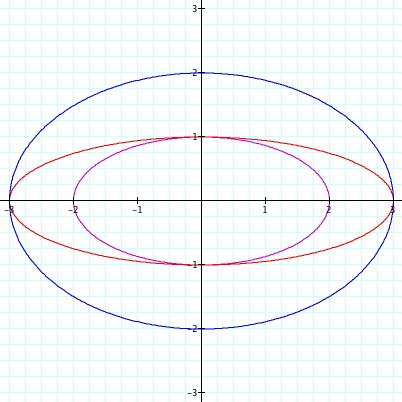
It is looks like when a 0 and b 0, we get ellipses centered at the origin with one axis along the x-axis of length 2a, and the other axis along the y-axis of length 2b. We can check that the curves are ellipses by calculating their focal points.
For example, when a =2 and b = 1 (the purple curve in the above graph). We know that since the major axis is along the x-axis, both focal points must lie on the x axis. Also, they will be equidistant from the origin. No matter how close to the origin they are, they will be inside the ellipse, so the sum of the distances from each of the focal points to (2,0), will be 2*2 = 4. But in order for the curve to be an ellipse, every point on it must be equidistant from these focal points, so (1,0) is also equidistant from each of them. But since the focal points are along the x-axis and equidistant from the origin, they must each be a distance of 2 away from (1,0). This gives us a right triangle with hypotenuse 2 and height 1, so we can use the Pythagorean Theorem to calculate its length to be 
. Therefore, we know that if this curve is an ellipse, its focal points lie at (,0) and (-,0). We can then check to see that the other points on the curve are have a sum distance of 4 from the focal points to ensure that it is an ellipse.
This method can be repeated for any of these curves, and even though the focal points change each time, the fact that the curve is an ellipse does not. The focal points will always be symmetric about the origin and along the major axis, which will be the x-axis when a is greater than b and the y-axis when b is greater than a.
Making a negative will simply reflect the ellipse across the y-axis, and making b negative will simply reflect the ellipse across the x-axis. In either case (or when they are both the case), the curve remains the same. Therefore, we get ellipses centered at the origin with one axis along the x-axis of length |2a| and the other axis along the y-axis of length |2b|.
We could also look at what happens when we multiply t by a constant instead of the whole function, giving us the following:
x = cos(at); y = sin(bt) for 0 t 2.
a = 2 and b = 1 in purple; a = 3 and b = 1 in red; a = 2 and b = 3 in blue.
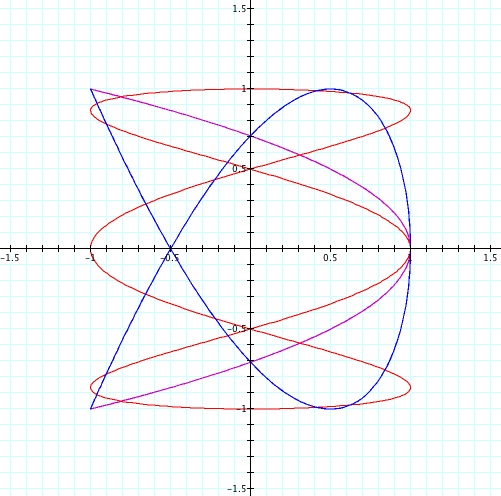
These curves can take many shapes, a few of which are shown in the graph above, but there are 2 things that they always have in common.
First of all, (1,0) is always on the graph. This is because t = 0 is always on the graph, and it will always give us x = cos(0) = 1 and y = sin(0) = 0.
Second of all, the curve will always be inscribed in the square with vertices (-1,1), (1,1), (1,-1), and (-1,-1). It will always touch at least one side of this square at the point (1,0), and may touch other sides, but it will never go beyond them. This is because the values both the sine function and the cosine function are always at least -1 and at most 1.