

The Bouncing Barney Problem can be written as follows:
Barney is in a triangular room with corners A, B, and C. He begins somewhere in the middle of the room and moves parallel to side AB until he hits a wall. he then moves parallel to side AC until he hits another wall, he continues this process, always moving parallel to the wall that he can walk along without causing him to back track, for an undefined amount of time. Will he ever return to his starting point, and if he does, how long will his path be?
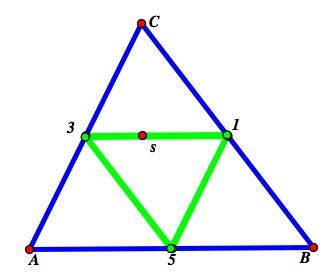
Here is one particular instance of the Bouncing Barney Problem where Barney starts at point s. He moves from s to 1, 1 to 2, 2 to 3, 3 to 4, 4 to 5, 5 to 6, and 6 back to s:
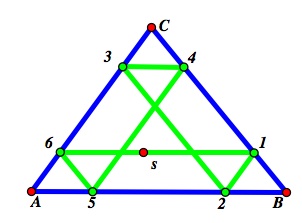
If you wish to see a GSP file where you can change the size and shape of the room as well as Barney's path, here is one:
The answer is yes, Barney will always return to his starting point. This is because (with 2 exceptions that we will cover later) the path that Barney travels is composed of seven triangles, all of which are similar to the original triangle, and at least 6 of which are congruent to each other, as can be seen below:
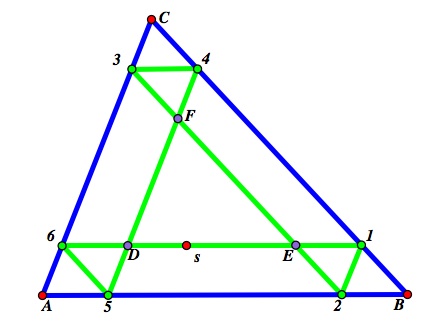
Simple proofs with parallel lines are sufficient to show that the following eight triangles are similar: ![]() ABC,
ABC, ![]() A56,
A56, ![]() 2B1,
2B1, ![]() 34C,
34C, ![]() D65,
D65, ![]() 1E2,
1E2, ![]() 43F, and
43F, and ![]() DEF.
DEF.
Once we prove the similarity of these triangles, we can prove that ![]() A56,
A56, ![]() 2B1,
2B1, ![]() 34C,
34C, ![]() D65,
D65, ![]() 1E2, and
1E2, and ![]() 43F are congruent simply by showing that |A5| = |2B| = |34| = |D6| = |1E| = |43|. This gives us the shape of the Barney's path, and it is cyclic, which proves that he returns to his starting point.
43F are congruent simply by showing that |A5| = |2B| = |34| = |D6| = |1E| = |43|. This gives us the shape of the Barney's path, and it is cyclic, which proves that he returns to his starting point.
Furthermore, showing the congruency of ![]() A56,
A56, ![]() 2B1,
2B1, ![]() 34C,
34C, ![]() D65,
D65, ![]() 1E2, and
1E2, and ![]() 43F is sufficient to show that this path is always equal to the perimeter (with 1 exception that we will cover later. This is because |AB| = |61| + |34|; |BC| = |23| + |56|; and |AC| = |54| + |21|. This also be shown using simple proofs with parallel lines.
43F is sufficient to show that this path is always equal to the perimeter (with 1 exception that we will cover later. This is because |AB| = |61| + |34|; |BC| = |23| + |56|; and |AC| = |54| + |21|. This also be shown using simple proofs with parallel lines.
Because these proofs come from the fact that the lines are parallel, the angles of the triangle do not change the problem. Everything stated is true for all triangles regardless of whether or not they are right, obtuse, isosceles, or equilateral.
Now we will look at some interesting cases: 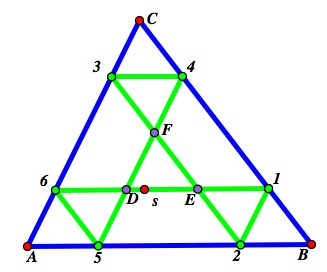
If |B1| = ![]() |BC|, we get a case of seven congruent triangles:
|BC|, we get a case of seven congruent triangles: ![]() A56,
A56, ![]() 2B1,
2B1, ![]() 34C,
34C, ![]() D65,
D65, ![]() 1E2,
1E2, ![]() 43F, and
43F, and ![]() DEF. The reason that
DEF. The reason that ![]() DEF is congruent to the other 6 is because, as we have already established, |AB| = |61| + |34|. |B1| =
DEF is congruent to the other 6 is because, as we have already established, |AB| = |61| + |34|. |B1| = ![]() |BC|, and
|BC|, and ![]() 2B1 similar to
2B1 similar to ![]() 34C tells us that |61| =
34C tells us that |61| = ![]() |AB|. Therefore,
|AB|. Therefore, ![]() |AB| = |34| = |6D| = |E1| = |DE|. Since we already showed that
|AB| = |34| = |6D| = |E1| = |DE|. Since we already showed that ![]() DEF is similar to these other triangles, we know that in this case it is congruent to them as well.
DEF is similar to these other triangles, we know that in this case it is congruent to them as well.
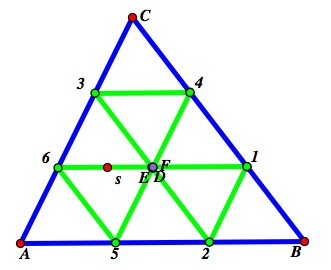 If |B1| =
If |B1| = ![]() |BC|, then D, E, and F merge to one point, causing the middle triangle to disappear. We get a set of nine congruent triangles. These nine triangles are:
|BC|, then D, E, and F merge to one point, causing the middle triangle to disappear. We get a set of nine congruent triangles. These nine triangles are: ![]() A56,
A56, ![]() 2B1,
2B1, ![]() 34C,
34C, ![]() D65,
D65, ![]() 1E2,
1E2, ![]() 43F,
43F, ![]() 6D3,
6D3, ![]() 52D, and
52D, and ![]() D14. We already know that
D14. We already know that ![]() A56,
A56, ![]() 2B1,
2B1, ![]() 34C,
34C, ![]() D65,
D65, ![]() 1E2, and
1E2, and ![]() 43F are congruent, and we can show the other 3 are congruent by SSS. We do this by showing that |36|, |14|, and |52| are exactly
43F are congruent, and we can show the other 3 are congruent by SSS. We do this by showing that |36|, |14|, and |52| are exactly
![]() of their respective sides, and the other three sides of the triangles are shared with the triangles that we already know are congruent.
of their respective sides, and the other three sides of the triangles are shared with the triangles that we already know are congruent.
 If |B1| =
If |B1| = ![]() |BC|, then we get many points that converge onto each other. 1, 2, and E converge; 3, 4, and F converge; and 5, 6, and D converge. This causes Barney's path to become the medial triangle. This is the only case where his total path is not equal to the perimeter; it is equal to half of the perimeter. This is because his path is now simply
|BC|, then we get many points that converge onto each other. 1, 2, and E converge; 3, 4, and F converge; and 5, 6, and D converge. This causes Barney's path to become the medial triangle. This is the only case where his total path is not equal to the perimeter; it is equal to half of the perimeter. This is because his path is now simply ![]() 135. |31| =
135. |31| = ![]() |AB|; |53| =
|AB|; |53| = ![]() |BC|; and |51| =
|BC|; and |51| = ![]() |AC|. We also have a set of 4 congruent triangles in this case:
|AC|. We also have a set of 4 congruent triangles in this case: ![]() 135,
135, ![]() A53,
A53, ![]() 5B1, and
5B1, and ![]() 31C. We know they are congruent by SSS because the side lengths match
31C. We know they are congruent by SSS because the side lengths match ![]() |AB|,
|AB|, ![]() |BC|, and
|BC|, and ![]() |AC| respectively.
|AC| respectively.
Another way we can look at the Bouncing Barney problem is to extend the sides and look at what Barney's path would be if he started outside of the triangle. Here is what this would look like:
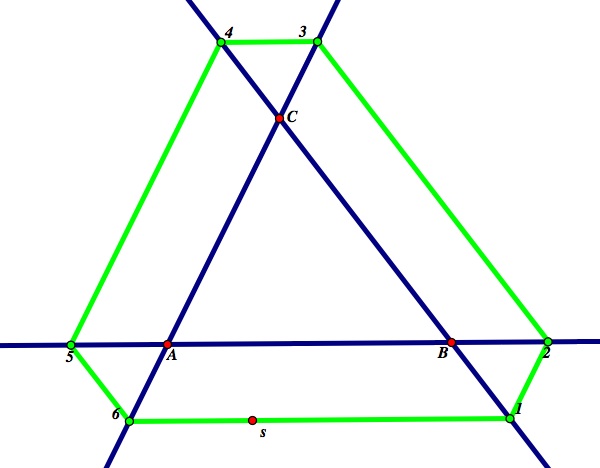
It is obvious that in this case, his path is longer than the perimeter of the triangle. However, if we consider some of the segments to be of negative length, his path still ends up being the perimeter of the triangle. These segments are |12|, |34|, and |56|. In order to show this, we first need to show that ![]() ABC is similar to
ABC is similar to ![]() A56,
A56, ![]() 2B1, and
2B1, and ![]() 34C, and the following triangles are congruent:
34C, and the following triangles are congruent: ![]() A56,
A56, ![]() 2B1, and
2B1, and ![]() 34C. This can be done using the same method as before. Once this is accomplished, we can show that:
34C. This can be done using the same method as before. Once this is accomplished, we can show that:
|AB| + |43| = |61|; |BC| + |65| = |23|; and |AC| + |12| = |54|. This is true because |43| = |B2|, |65| = |C4|, and |12| = |C3|
Therefore, the perimeter of ABC = |61| - |12| + |23| - |34| + |45| - |56| regardless of how far away from the triangle s is located.