is the standard form of a parabola, and
is the vertex form of a parabola.
We will explore how these formulas can be derived from one another and how their parameters are related. We will start with a derivation of the standard form from the vertex form:
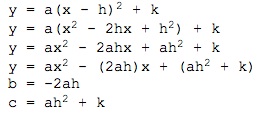
We will now derive the vertex form from the standard form:
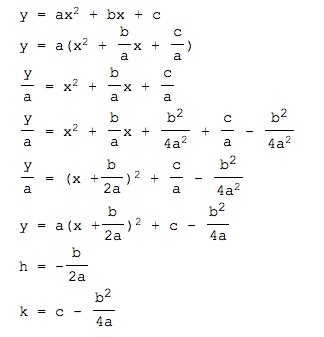
We can easily see that b = -2ah is equivalent to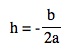 
Using this, we can see that our values of c and k are equivalent:
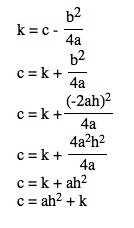
Now, lets look into why k and h are significant in the vertex form of a parabola: .
We know that 
is always either positive or 0. Therefore, when a is positive, we will have a minimum when x = h, and when a is negative, we will have a maximum when x = h. This tells us that the vertex will occur when x = h. The y value of the vertex will always be k because when x = h, will be 0, canceling out every term on the right hand side except k, so y = k. Thus, the vertex of a parabola in vertex form is always (h,k).