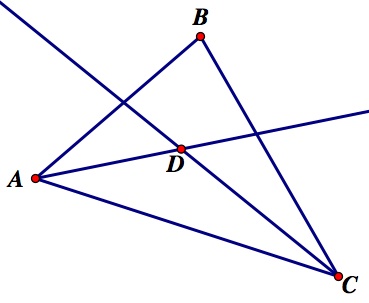
Proposition 1: The three angle bisectors of any triangle are concurrent, meaning that all three of them intersect.
Proof: given any triangle, ABC, we can take two angle bisectors and find they're intersection. It is not difficult to see that they always intersect inside the triangle. This is because they originate from the triangle's vertices and remain inside the triangle until they cross the opposite side. We will call they're intersection point D.
Our next step is to construct the segments through D at a perpendicular to the three sides of the triangle. Displayed in red, we use the intersections of these segments with the sides of the triangle to get points E, F, and G as such:
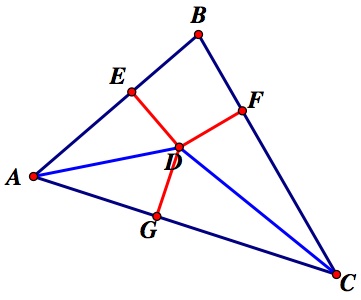
We know that 
EAD 
GAD by construction, and DEA and DGA are both right, so ADG ADE = 
- EAD - DEA. We then see that 
EAD GAD by ASA.
Similarly, GCD FCD by construction, and DFC and DGC are both right, so CDG CDF = - GCD - DFC. We then see that GCD FCD by ASA.
This tells us that DE = DF = DG. This will be important later in our investigation of the Incenter.
We can now construct segment DB.
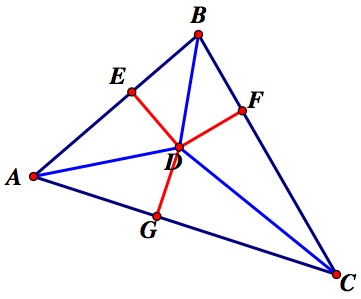
We can see that DBF and DBE are both right triangles with the same hypotenuse and the same length of one of their legs because DE = DF. We know from the Pythagorean Theorem that BE = BF. Therefore, DBF DBE by SSS. This tells us that DBF DBE, which means that the angle bisector of ABC always runs through point D. Thus, the angle bisectors of any triangle are concurrent.
Proposition 2: The point of concurrency of the angle bisectors of any triangle is the Incenter of the triangle, meaning the center of the circle inscribed by that triangle.
Proof: In our proof above, we showed that DE = DF = DG where D is the point of concurrency of the angle bisectors and E, F, and G are the points of intersection between the sides of the triangle and the perpendicular to those sides through D. This tells us that DE is the shortest distance from D to AB, DF is the shortest distance from D to BC, and DG is the shortest distance between D and AC. From this, we can see that the circle with center D and radius DE = DF = DG is the circle inscribed by triangle ABC, and the proof is finished.
Proposition 3: The area of a triangle is equal to half of the perimeter times the radius of the inscribed circle.
Proof: We return to the previous diagram:
We can see that the area of ABC = the area of ABD + BCD + ACD.
The area of ABD = 
AB x ED. The area of BCD = BC x FD. And the area of ACD = AC x GD.
So ABC = AB x ED + BC x FD + AC x GD. But ED = FD = GD,
So ABC = AB x ED + BC x ED + AC x ED
So ABC = (AB + BC + AC)(ED). And the perimeter of ABC = (AB + BC + AC), and the radius of the inscribed circle = ED, so the area of a triangle is equal to half of the perimeter times the radius of the inscribed circle.