A pedal triangle is formed from a triangle and a pedal point, and it is an easy construction. First, one should extend all of the sides of a triangle into full lines. Then, One draws a perpendicular line from each of those lines through the pedal point, as seen below:
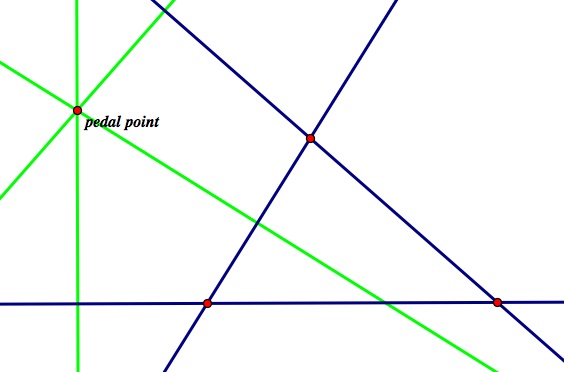
Next, one only has to draw the intersection of the lines through the pedal point (green) with the sides of the original triangle (blue). We are only interested in the intersections of the instances where the lines are perpendicular. This is shown below with the pedal triangle in black:
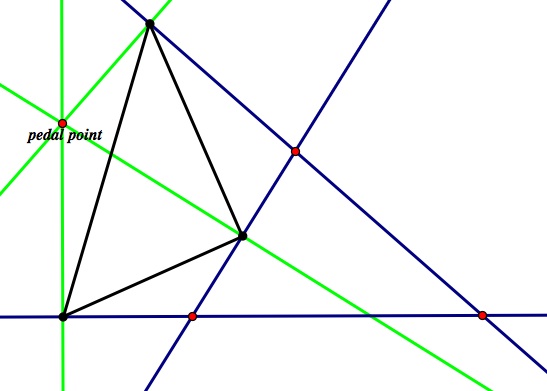
Not only can we get pedal triangles for any triangle, but we can move the pedal point around for particular triangles to see how the pedal triangles change. Here is a GSP file that contains a pedal triangle tool:
In most cases the pedal triangle is actually a triangle, but in some cases, the three points are colinear. In this case we can refer to the pedal triangle as a degenerate triangle.
If one stops and looks for a minute, he or she can see that the pedal triangle is always degenerate when the pedal point is one of the vertices. This is because when the pedal point is on a vertex, two of the three points are the same point, which is the pedal point. However, these are not the only cases where the pedal triangle is degenerate.
When the pedal point is anywhere on the circumcircle of a triangle, the pedal triangle is degenerate. Here is a GSP file that demonstrates this:
Note: One can drag the vertices of the triangle around in this file to test this fact for any triangle.
I am not able to generate my own mathematical proof that this is true for every triangle or that this is the only way to get a degenerate pedal triangle.
Obviously, whenever these three points form a degenerate triangle, they are colinear. The line that they form in this case is called the Simpson Line. There are three cases with every triangle where the Simpson Line is the same as one of the sides of the triangle (one for each side). Here is such an example:
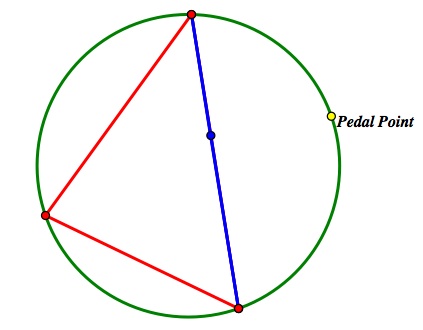
This is the case when two of the three points on the pedal triangle are also vertices of the triangle. In an acute triangle, the third point is always in the middle of that side.
The Simpson Line is on a side of the triangle when the pedal point is on the intersection of the circumcircle and one of three particular lines. Each of these three lines is formed from the circumcenter of the triangle and one of the vertices of the triangle.
For example, if we wanted to find the point where the Simpson line is on side AB of 
ABC, we would first find the line generated by the circumcenter of ABC and point C. this line intersects the circumcircle in 2 different places, one of which is point C, so we place our petal point on the other intersection, and our Simpson Line ill be on side AB
Here is GSP file that shows these three intersections in brown and the special lines in yellow:
Simpson Line on Triangle's Side
Once again, I do not have a mathematical proof of this, I simply have observations through GSP.