

Problem: Graph logx/log a and ln x/ln a for different values of a
In this write up, I will compare the graph y = log(x)/log(a) and the graph y = ln(x)/ln(a), when a is many different values.
First, let's try a = 2, and see what we come up with:
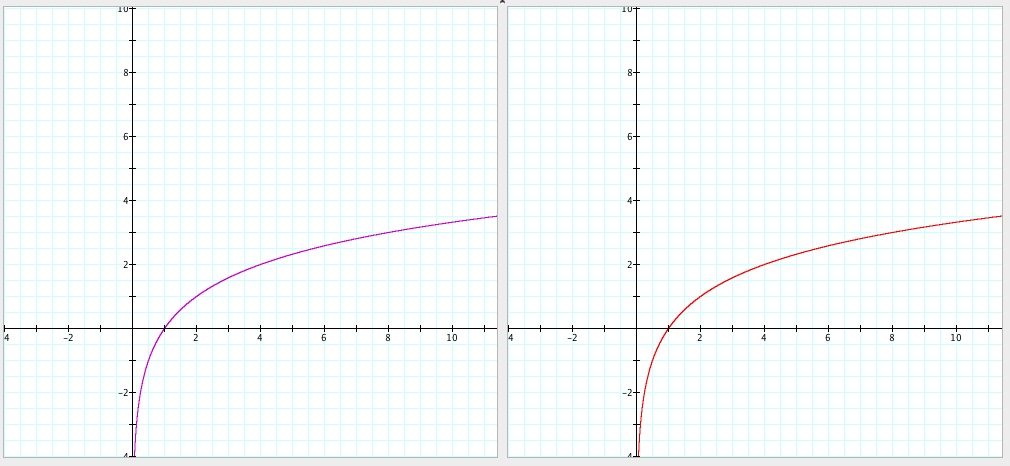
Now let's try with a = e:
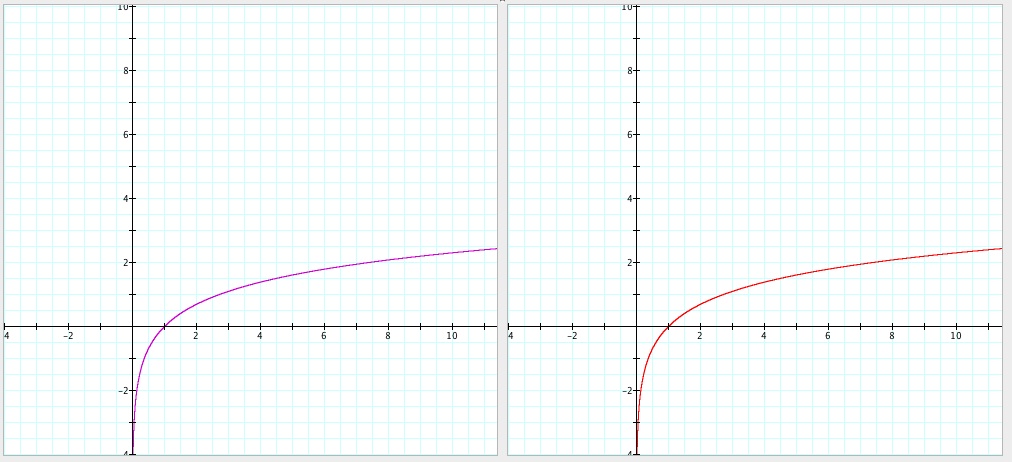
Third, let's try with a = 3.
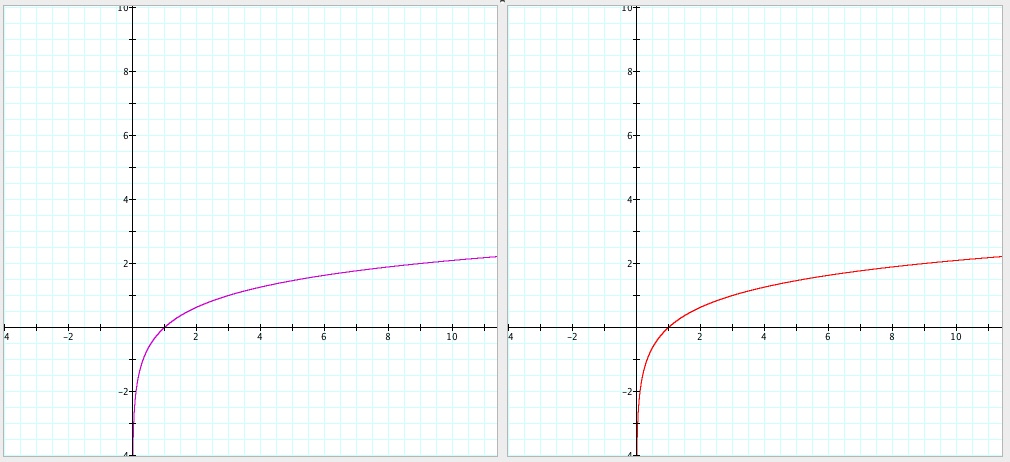
What about with a = 5?
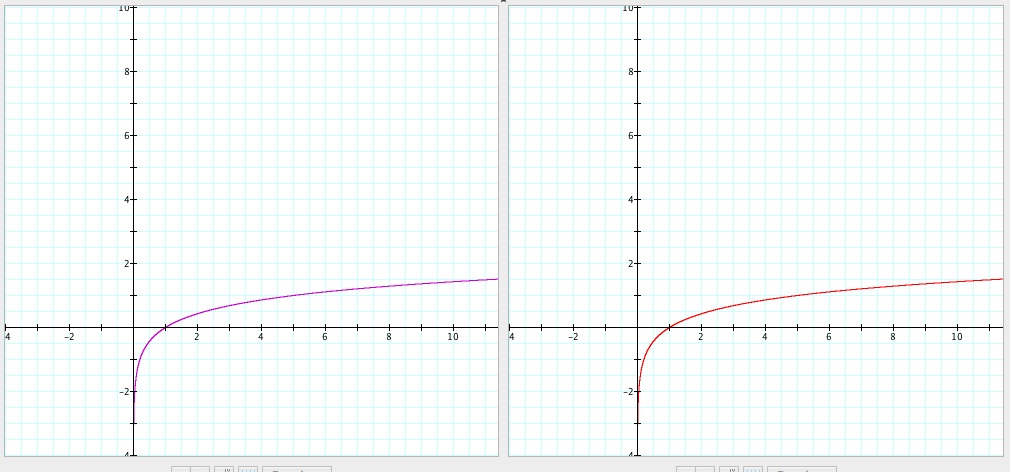
Hmmm... This is very interesting. What about a = 8?
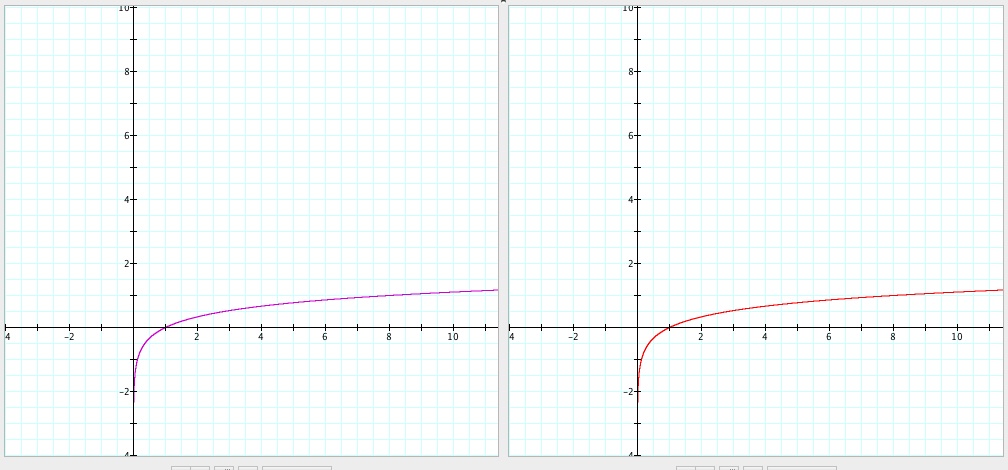
One final shot with a = 10.
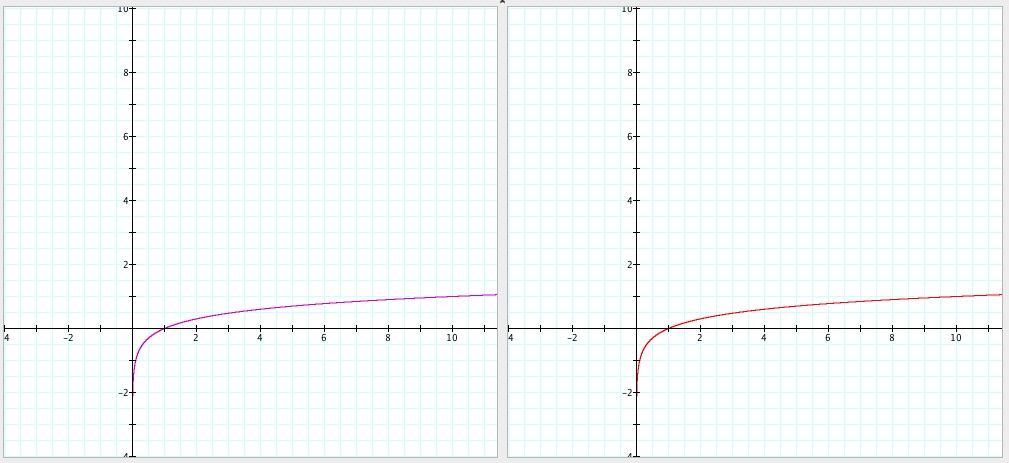
Finally, Here is an animation of the graphs when a is between 1 and 10:
Before I get into comparing the two graphs in each case, I will state that as a increases, and as x>1, the right end of the graph is getting closer and closer to one. This makes sense that as a gets larger, the log a is getting closer to the value of log x for larger x and thus the quotient is becoming closer to 1. This may seem obvious but it is an important property to notice with these types of graphs.
Now what do I notice when comparing the two graphs. Well, unless I am blind, it seems like these two graphs are the same for all a. Comparing the values on each graph, this seems like a reliable conjecture. However, this seems like something that needs to be mathematically proven, and thus I have done so below (done in gsp for better viewing):

What an amazing proof! It seems that from the generality of this proof, you could do this for any base of logarithms.