

Problem: Produce several ( 5 to 10) graphs of
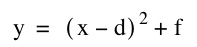
on the same axes using different values for dand f. Does varying d change the shape of the graph? the position? Does varying f change the shape or position of the graph?
Plot the points (d, f) on your graphs using
This is the GC 3.5/4.0 "2-vector" input and is essentially a parametric equation for a point.
Write-up:
I will present a few different values of d and f to show the variation that occurs.
First, I will show below the graph that has both d and f at zero. As expected, this is just a graph of a parabola that has its vertex at the origin (y=x2).
Second, what occurs when d = 1, and f = 1 so that we have y = (x-1)2+1?
At a first look, the graph has moved. The vertex has moved from (0,0) to (1,1). A first conjecture can be that (d,f) represent the vertex of the function. Perhaps d is responsible for a move in the x direction and f is responsible for a move in the y direction. More graphs are needed to see if these are reasonable conjectures.
The third graph displayed below occurs when d = 0 and f = 1, giving us y = (x-0)2+1. Will it do what we expect it to after the last graph?
After viewing this graph, it seems as though my conjecture may be correct. In this case, d=0 and the graph's vertex did not move in any horizontal manner. However, f was equal to one and the vertex has moved up one unit in the vertical since, now at (0,1). It seems as though the d and f are just providing us with shifts vertically and horizontally, not changing the width or concavity of the graph.
The fourth graph displayed below occurs when d = 1 and f = 0, giving us y = (x-1)2. Here, I would expect the parabola to move horizontally in a positive manner, now having a vertex at (1,0). Will that happen?
At first glance, indeed, the parabola has moved in the manner that I had guessed. It is now really appearing like d and f only provide us with vertical and horizontal shifts of the graph. Let's try a few more though, before we go to crazy!
The fifth graph displayed below occurs when d = 5 and f = 5, giving us y = (x-5)2 +5. Here, I would expect the parabola to move horizontally and vertically in a positive manner, now having a vertex at (5,5). Will that happen?
Success! The fifth graph provides us with a parabola that has a vertex at (5,5). Although this is not a mathematical prove, we are close to convincing ourselves that this is the behavior being exhibited when changing d and f. However, what happens when you change d or f to be negative?
The sixth graph displayed below occurs when d = -2 and f = 0, giving us y = (x-(-2))2 +0. Here, I would expect the parabola to move horizontally in a negative manner, now having a vertex at (-2,0). Will that happen?
Even when using negative d, it seems that my conjectures above are true. There seems to be only one thing left to check or explore with an example. What happens if f is negative? We should expect more of the same.
The last graph displayed below occurs when d = -2 and f =-5, giving us y = (x-(-2))2 -5 . Here, I would expect the parabola to move horizontally and vertically in a negative manner, now having a vertex at (-2,-5). Will that happen?
And again, my conjecture is shown to work in this case, we have a vertex of a parabola at (-2,-5) given d is equal to -2 and f is equal to negative 5.
Overall conclusions: From viewing 7 different graphs, each having different d and f, I have concluded that changing the values of d and f will only change the position of the graph, with d and f being the coordinates of the vertex of the parabola. This does make some sense as the form (x-d)2 + f is known as the vertex form. It does not, however, appear like the change of d and f change anything about the shape of the graph. In each case, the direction of the graph's concavity was the same (it did not change to negative, go sideways, or anything like that). The width of the "openness" of the parabola did not change either, at least from the 7 views that I saw. I suppose that this would be expected given that changing d and f do not change the fact that a=1 in all cases when we factor out and get the form ax2 + bx + c. This is very useful to know if one was looking for the vertex of a parabola but did not want to change the shape of the graph.