

Problem: Construct a tangent circle.
Steps:
1. Construct two circles. In this case, I will have one within the other:

2. What I want is a circle that is tangent to the outside of the inner circle and also tangent to the outer circle. To construct such a circle choose an arbitrary point on the outer circle and draw in the radius. Mark off a distance equal to the radius of the inner circle.
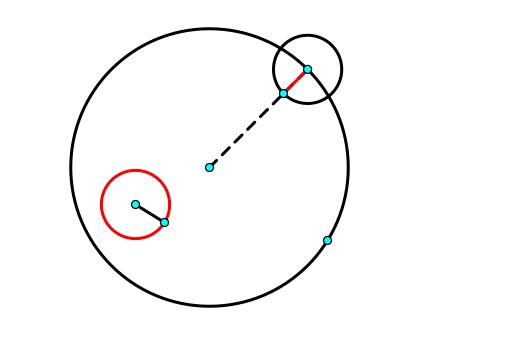
3. Connect the two points labeled A and C on the circles. Then make a triangle by drawing the perpendicular Bisector of AC, which will intersect with the radius of the big circle.
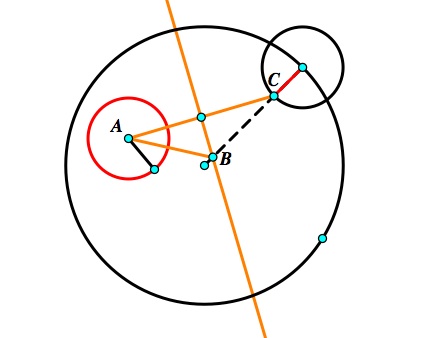
4. Use segment BD as a radius of your new circle and construct the circle. This will be tangent to the outside of the black circle since the radii of the black circles is the same and segment AD would be the same as segment BC the radius of circle C.
A tangent circle has been constructed. However, what can we do with this information? What more can I investigate? Well, I have chosen to Investigate, discuss, and state conjectures about the loci of the centers of the tangent circle.
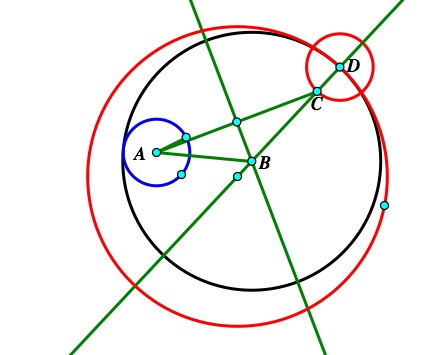
Case 1: One of the circles is completely within the other. See image below (The highlighted figure is the locus).
Just from looking at the image, it appears that the locus forms an ellipse.
Proof: For this to be an ellipse, there needs to be a constant sum of the distances mBE and mBA. We already know this is true since ED is constant and mED – mAD = mEB + mBC, but mBA and mBC are the same since the triangle is isosceles as desired.
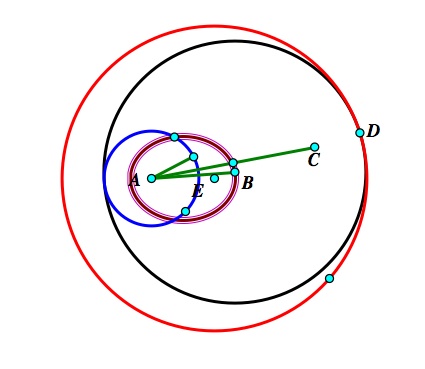
Case 2: The circles overlap one another. See image below (The highlighted figure is the locus).
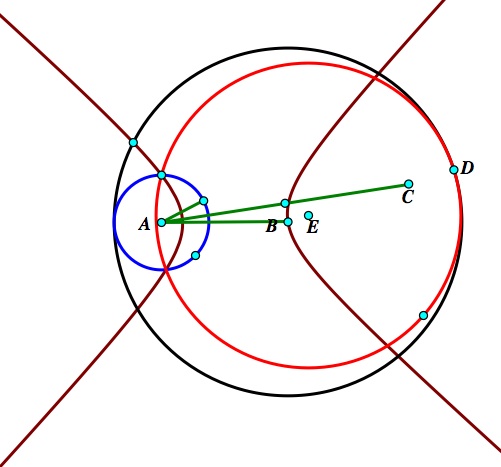
Again, just from looking at the image, it appears that the locus forms a hyperbola. How can we show this?
To show that the trace is a hyperbola, it must be shown that that the distance from A to B subtracted from the distance from the center of the red circle (which I will call point E) to B is a constant value. Notice that ED is the radius of the red circle, which we are holding constant. The only thing we are changing is the position of D. It was shown earlier that mCB = mAB. This implies that mBD = mCB +mCD, subtracting mCD (distance equivalent to the radius of circle C) from both sides yields mAB = mBE + mEC, or, mAB – mBE = mEC. Of course, mEC is a constant since we are not changing the distance in either radius.
Case 3: The circles are completely disjoint.
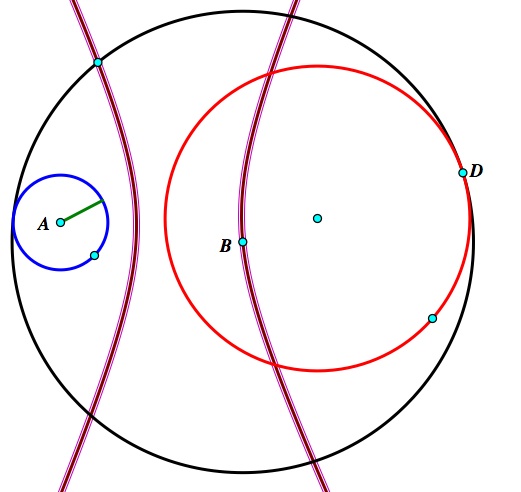
Like in case 2, it seems like the locus forms a hyperbola.
To show that the trace is a hyperbola, the exact same argument as in Case 2 can be used.
Overall this was probably the most challenging construction and write-up of the semester. Geometry has always been my "weakest" mathematical area, but this activity certainly helped me deal with the topics of tangency, ellipse, hyperbola, focus, locus, etc. From a pure mathematical perspective this was a very good learning experience. As for pedagogically, I could see something like this being used in the classroom to help students learn the concepts behind tangent circles. However, caution must be taken to make sure that students aren't lost, as one missed step of not understanding why something is taking place can bring down the entire process. Also, dynamically seeing the locus change from an ellipse to a hyperbola as the inner circle begins to overlap the outer circle once again shows the importance of using technology in these situations versus giving them a textbook with pure definitions and letting them fend for themselves! All and All, I think this was a good learning experience for me!