

Problem:
Given acute triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully.
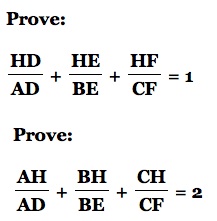
First, we must create an acute triangle ABC with Orthocenter H. The orthocenter is the point of concurrency or the common intersection of the three lines containing the altitudes. An acute triangle with Orthocenter H is shown below:
As in a Previous write-up, I am using GSP for the formulas and will paste the screenshot to here. First to prove proposition one.

Now we want to prove proposition 2:

Interestingly, though, we were asked to prove this just for acute triangles. This begs the question: Why not right or obtuse triangles?
For right triangles, we would have a situation shown below:
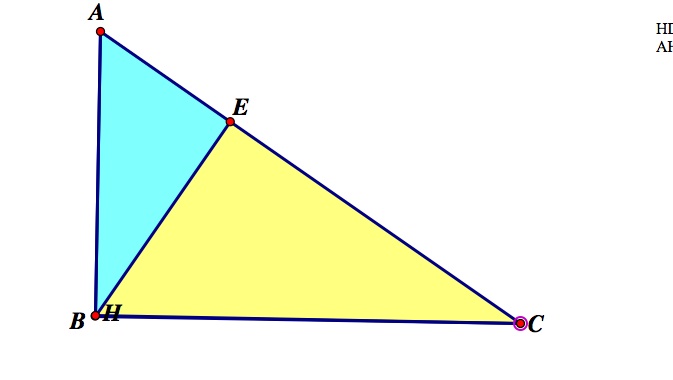
Here, the orthocenter is actually at the right angle, and so there are no such sides as "HD" and thus the statements are meaningless.
The same is true with obtuse triangles. In fact, the orthocenter goes outside of the triangle and thus makes the calculations even less meaningful in this case, as the side lengths are not defined (well, if they were, they'd be negative, which there is no defined "negative side length"). For instance HD/AD would be greater than one, thus making the proposition one impossible unless there were negative lengths.