

Problem: Pedal Triangles where pedal point is at different centers of the Triangle.
First, we should define what a pedal triangle is: Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
The following image shows the Pedal point within it's origin triangle:
As you can see, the entirety of the Pedal triangle is found within the original triangle. Is this true for every case where P is within the original triangle? Even in Right and Obtuse triangles? You can play by moving around pedal point P in the GSP file attached here. This does not seem to be true when the original triangle is an obtuse triangle.
When the Pedal point is outside of the original triangle, it appears that any number of things can happen to the pedal triangle, as shown here:
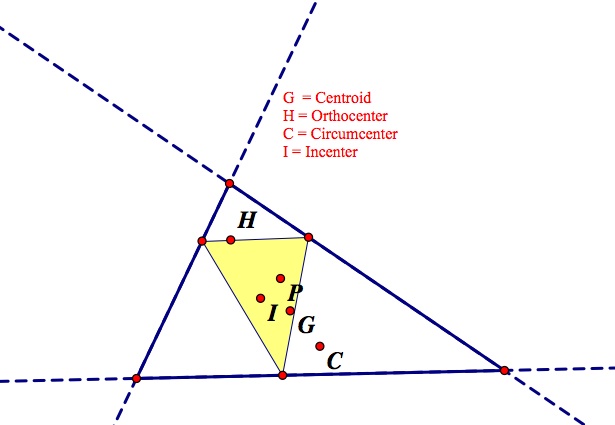
So what happens when the Pedal Point is at the Centroid? Here are two images that show different situations of this (one acute and one obtuse triangle).
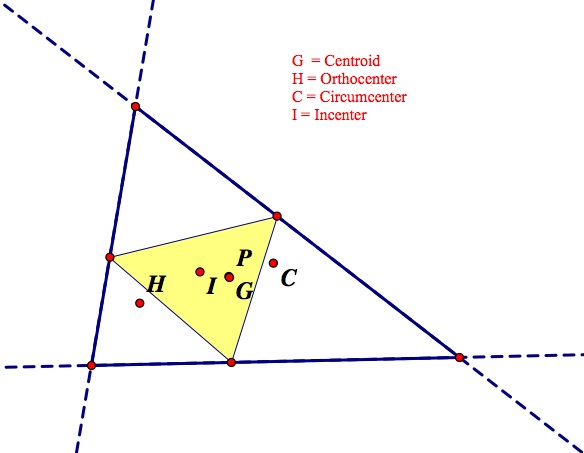
Upon my explorations of having the centroid and the Pedal point always in the same location, it appears that the pedal triangle will always remain entirely in the original triangle when the pedal point is at the centroid. I explored with many different types of triangles and none of them seem to have ended with a situation outside of the original triangle.
What happens when the Pedal Point is at the Orthocenter? Here are two images that show different situations of this (one acute and one obtuse triangle, the obtuse triangle having the orthocenter outside the initial triangle).
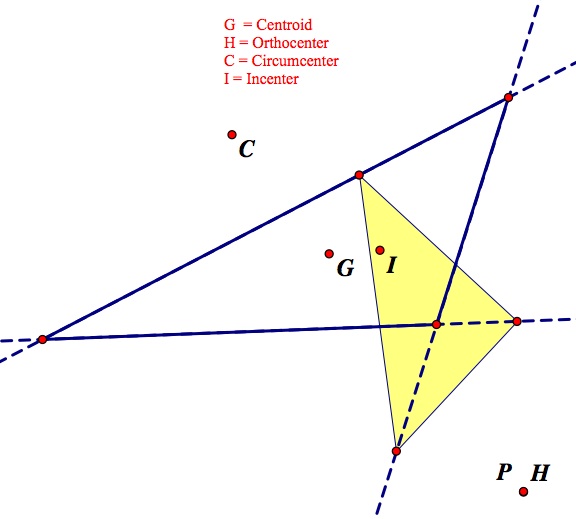
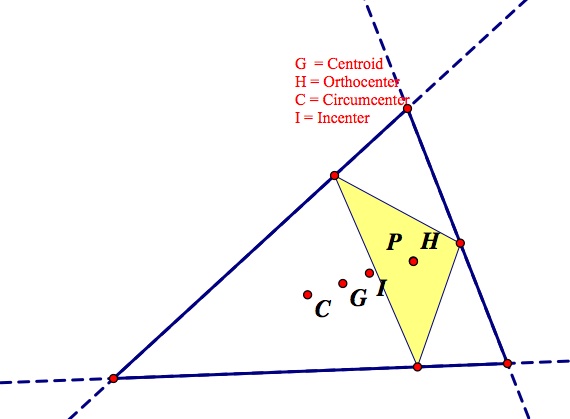
The case of the orthocenter was interesting because in this case when the triangle was acute, the orthocenter was within the original triangle but when the original triangle was obtuse, the orthocenter landed outside of the original triangle. Explorations of triangle centers from assignment number 4 are a good place to look for the activity of the orthocenter. In this case, unlike when the pedal point was at the centroid, the pedal triangle actually partially leaves the original triangle. Wildly varying the sides of the triangle will give you many different looks for the pedal triangle, but it is never entirely outside of the triangle, at least from my explorations, even when the orthocenter is a good distance away from the original triangle.
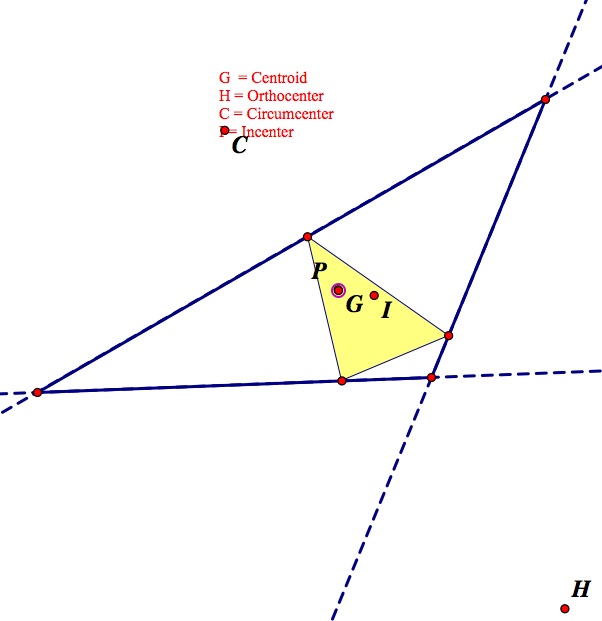
What happens when the Pedal Point is at the Circumcenter? Here are two images that show different situations of this (one acute triangle, on obtuse, In the obtuse triangle the circumcenter was outside the triangle).
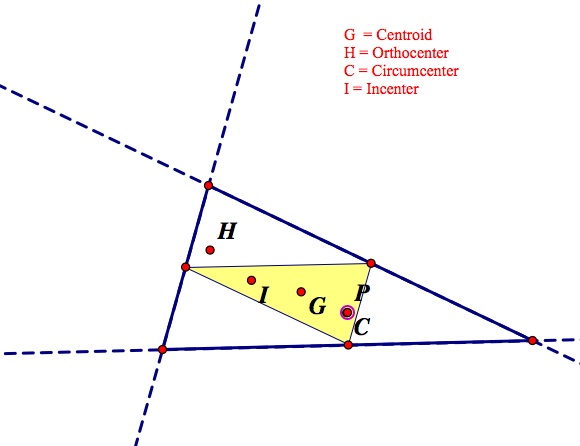
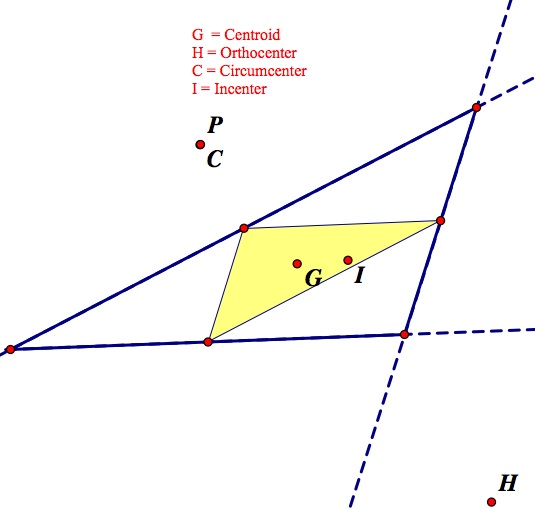
In this case, when the pedal point was located at the circumcenter, even when the circumcenter was outside of the original triangle, the pedal triangle remained within the original triangle. I varied the triangles widely to see if there was a case where the pedal triangle seeped outside of the original, but I did not find any of these cases. This should come as no surprise, though, as the circumcenter is created by the perpindicular bisectors, which else have a part in the creation of the pedal point and triangle.
What happens when the Pedal Point is at the Incenter? Here are two images that show different situations of this (one almost right triangle and one acute triangle).
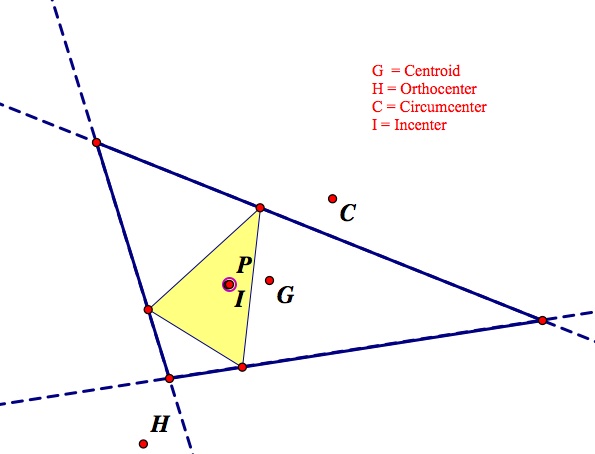
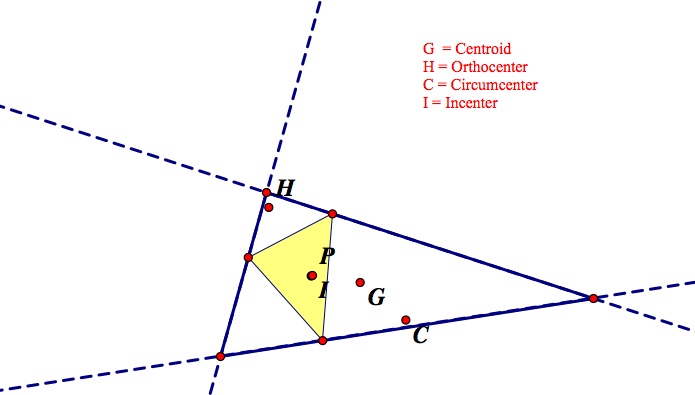
Once again, in both cases I found that the pedal triangle remained completely within the original triangle. There is good reason for this, though, as the Incenter is always within the triangle making it even more likely for the pedal triangle to stay within the triangle (since the incenter relies on the angle bisectors and is equidistant from all 3 sides, making it stay within the triangle).
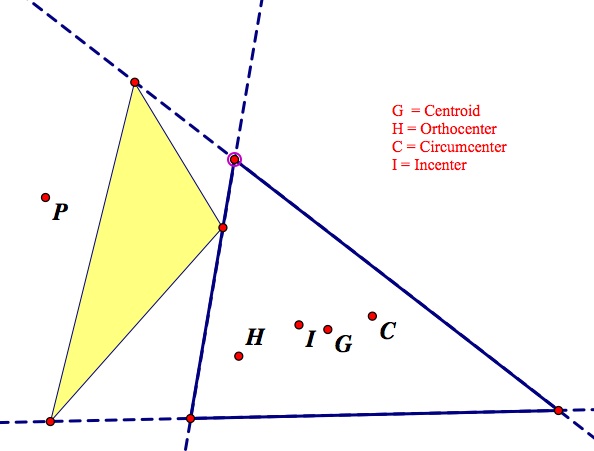
What if the pedal point lands on the center (N) of the nine-point circle? I have two images here from my explorations:
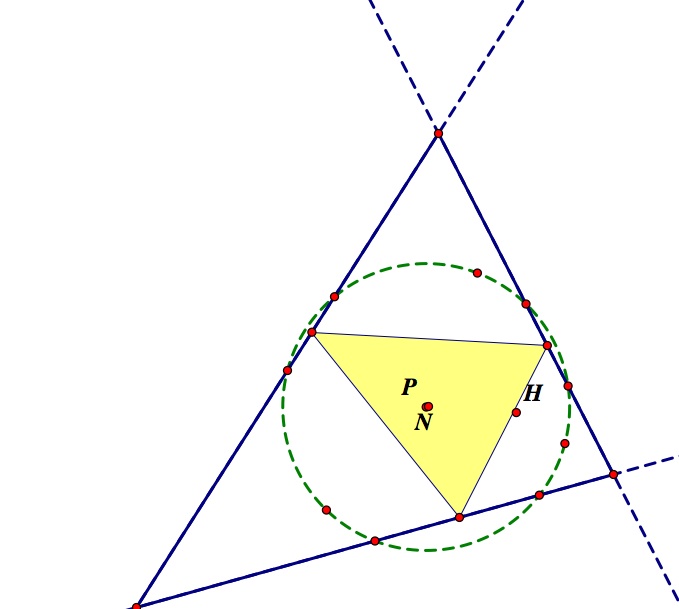
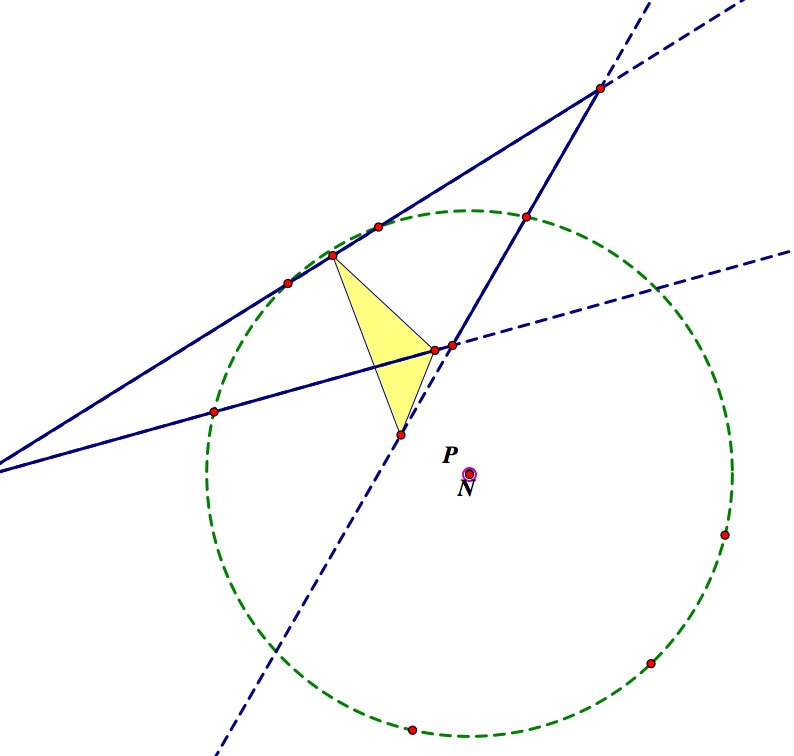
Here we can see that in the case where the center of the nine-point circle is within the original triangle, we have the pedal triangle staying within the original triangle when placed at N. However, the example on the right shows a dramatic example of what occurs when the N is outside of the original triangle and here part of the pedal triangle seeps outside of the original triangle.
Overall, the pedal triangle performs very interestingly when placed at the different centers in reference to a given triangle. It is not always guaranteed that the pedal triangle will stay within the given triangle when the pedal point is placed at one of the centers. However, at no point of my explorations did I ever see a pedal triangle go completely outside of the original triangle when the pedal point was placed at one of the circles that was discussed in this write up. Although I did not see it, it is always possible that I have missed something and this can lead to further exploration. For now, I'll leave that to another person and give a "To be continued..." cliffhanger.