Untitled Document

This unit is designed for 10th grade geometry students. Students should already be familiar with basic properties of triangles (angle measurements, types of triangles, similar and congruent triangles). It is a 12 day unit on proofs that go along with properties of triangles. There are periodic quizzes that allow the teacher to check the progress of the students' learning during this unit. The combination of the scores from the quizzes will be counted as one test grade for the semester.

Goal: students should know all the triangle centers, properties of triangles, be able to use the proper vocabulary when describing properties and parts of triangles, and be able to prove the Pythagorean theorem using 3 congruent squares
Day 1: Centers of Triangles
Day 2: Other cevians (Ceva's theorem)
Day 3: Quiz
Day 4: 9-Point Circle
Day 5: Euler Line
Day 6: Quiz
Day 7: Locus day 1
Day 8: Locus day 2
Day 9: Quiz
Day 10: Pythagorean relations
Day 11: Pythagorean relations
Day 12: Quiz

Goal: students should know how to create the 4 different centers of triangles (on GSP as well)
Lecture: on the centers, how to create each one, and different outcomes due to different types of triangles (equilateral, isosceles, scalene)

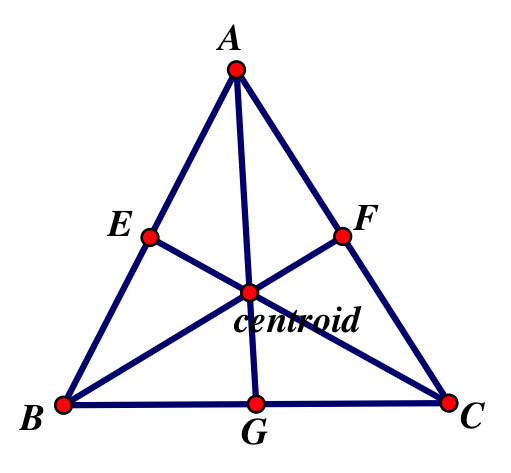
Centroid:
E= midpoint of AB
F= midpoint of AC
G= midpoint of BC
E, F, and G all meet in the center of the triangle at the point called the centroid. This is the center of mass of triangle ABC. The centroid crosses each median 2/3 of the way down.

Incenter:
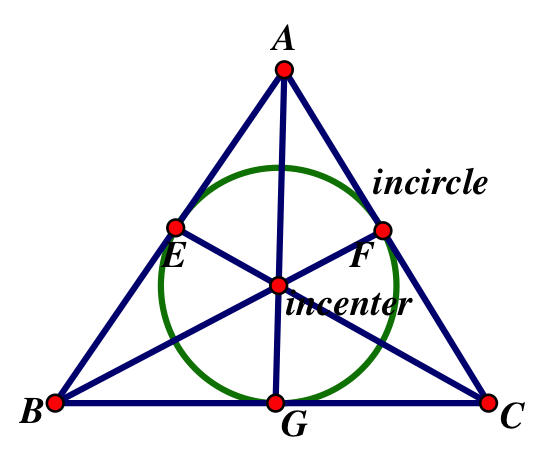
G= the point in which the bisector of angle A meets side BC
F= the point in which the bisector of angle B meets side AC
E= the point in which the bisector of angle C meets side AB

AC, BF, and AG all meet at a point called the incenter. This point is equidistant from all the sides so a circle with a center at the centroid is called the incircle, which touches all the points E, F, and G. The points from incenter to E, incenter to F, and incenter to G are all radii and equivalent.

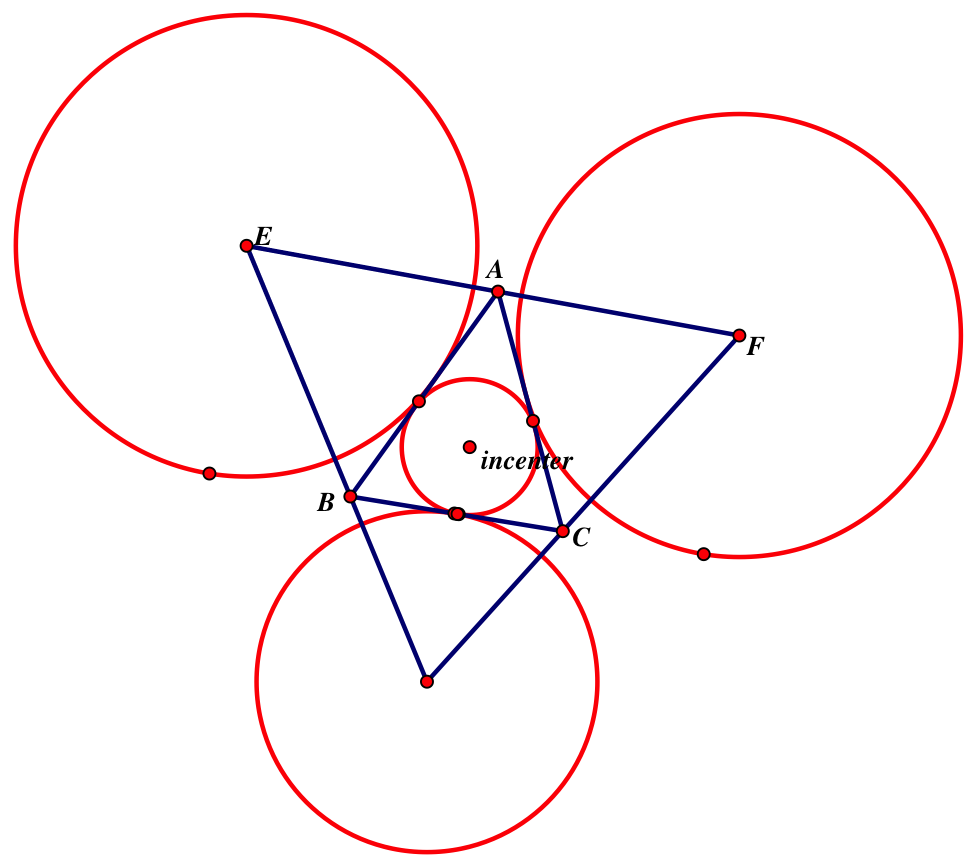
Along with the incenter of a triangle, there are also excenters, E,F, and G. We will go more in-depth into the excenter on day 2.

Angle bisectors do just this, they bisect an angle. While it is extremely easy to bisect and angle, it is much more difficult to trisect an angle. How would you go about trisecting an angle?

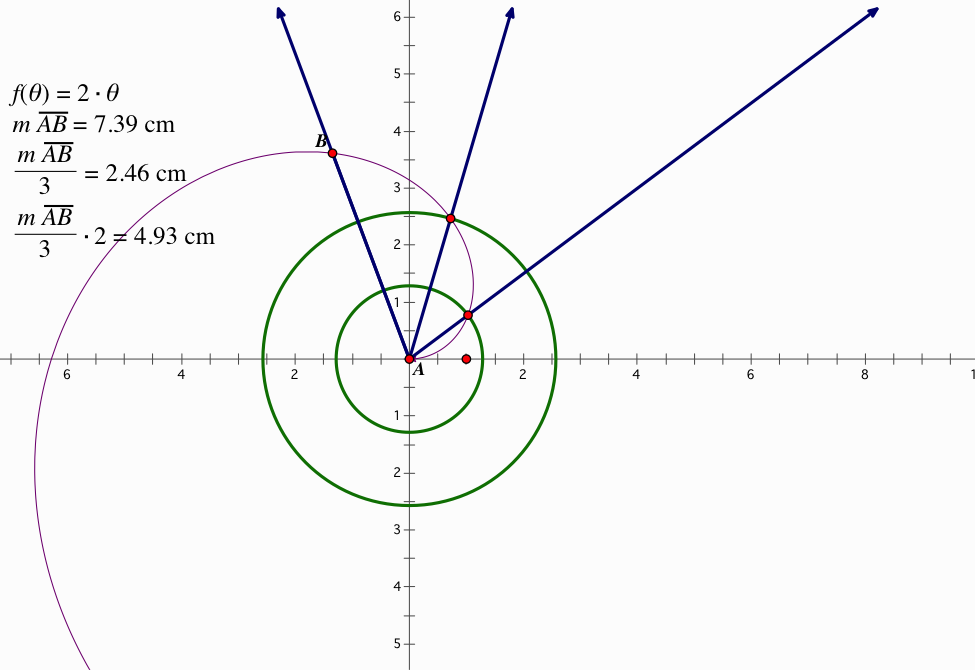
Keep in mind; we cannot trisect an angle (with the exception of 180 degrees) with the use of Euclidean tools, like a ruler and a compass. We must use new technology such as GSP to do so. This is one of the three famous geometric problems.

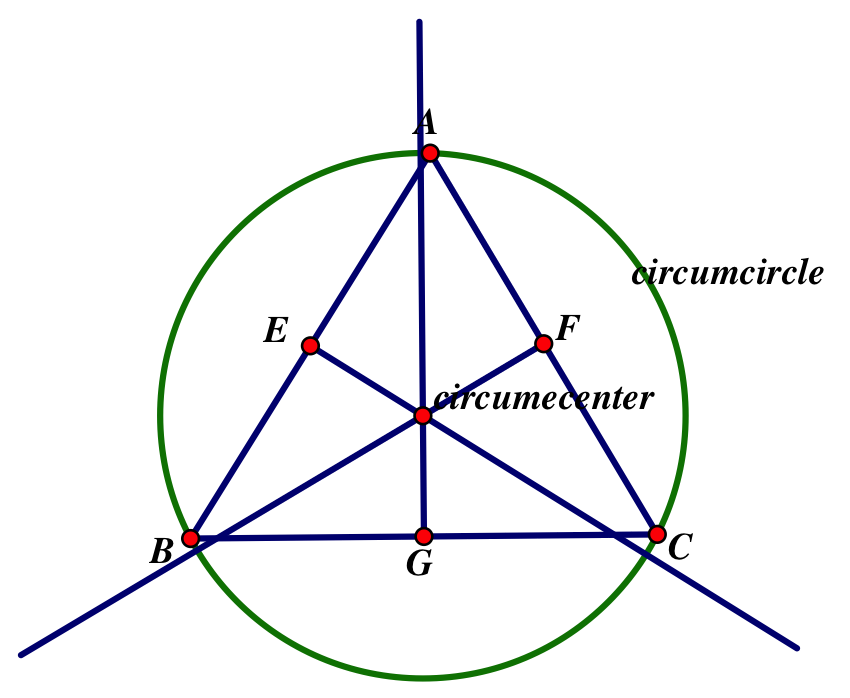
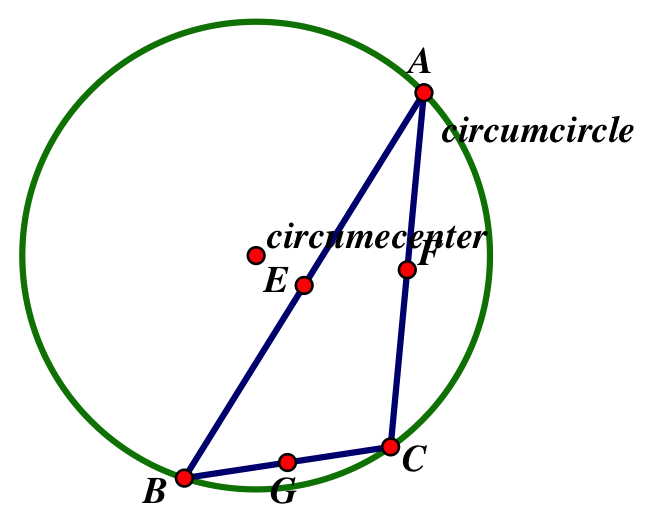
Circumcenter:
E= the perpendicular bisector of side AB
F= the perpendicular bisector of side AC
G= the perpendicular bisector of side BC

The perpendicular bisectors, also called altitudes, all meet at a point called the circumcenter. It is equidistant from all three vertices of triangle ABC and therefore a circle constructed with the center located at the circumcenter is called the circumcircle. Sometimes, depending on the triangle, the circumcenter will appear outside of the triangle.

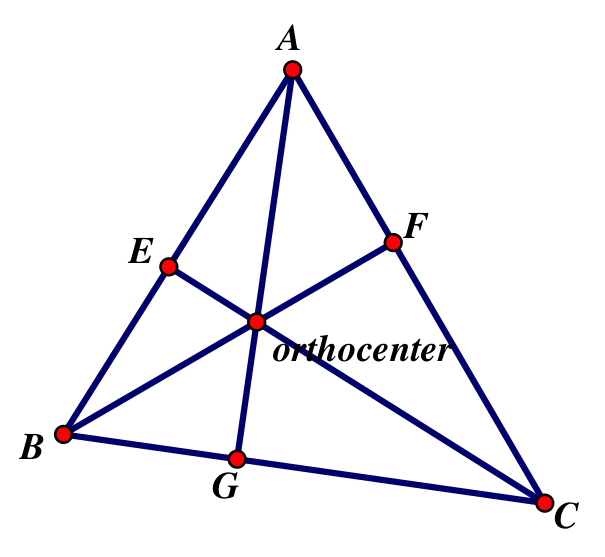
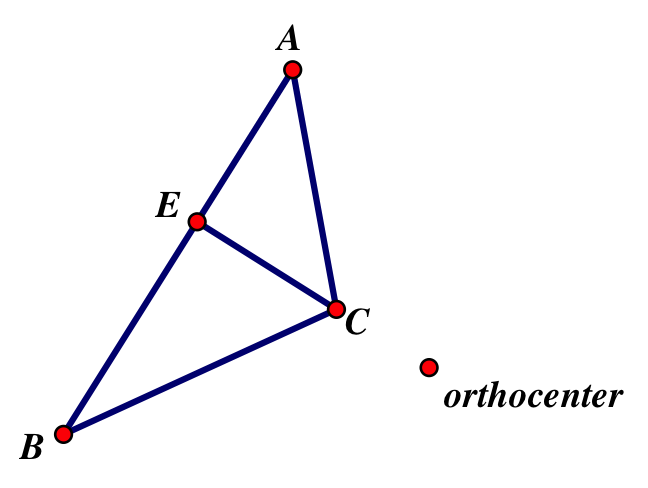
Orthocenter:
G= the point where the altitude through A meets side BC
F= the point where the altitude through B meets side AC
E= the point where the altitude through C meets side AB
The altitudes all meet at a point called the orthocenter. Like the circumcenter, the orthocenter will sometimes appear outside of the triangle.

1. cevians: A Cevian is a line segment which joins a vertex of a triangle with a point on the opposite side (or its extension).

2. angle bisectors: the line or line segment that divides the angle into two equal parts.

3. altitude: The altitudes of a triangle are the Cevians that are perpendicular to the legs opposite the given side

4. circumcircle: The circumcircle is a triangle's circumscribed circle, i.e., the unique circle that passes through each of the triangle's three vertices.

5. incircle: An incircle is an inscribed circle of a polygon, i.e., a circle that is tangent to each of the polygon's sides.

6. medians: A triangle median is the Cevian from one of its vertices to the midpoint of the opposite side.

11. circumcenter: the intersection of the three perpendicular bisectors of a triangle

Goal: for students to understand what an excenter is and how it relates to the original triangle and to understand Ceva’s theorem
Lecture: explain how to create an anticevian triangle and Ceva’s theorem

Recall this picture from day 1. The triangle EFG created by the excenters of ABC is called an anticevian triangle. The triangle formed by the inside points where the angle bisector meets the opposite side is called the cevian triangle.
There are several different anticevian triangles. Here are two that apply to yesterday’s lesson.
1. anticevian triangle of the incenter is the excentral triangle
2. anticevian triangle of the centroid is the antimedial triangle

Part II: Ceva’s Theorem
Proof: Given a triangle ABC, let the lines AO, BO, and CO be drawn from the vertices to a common point O to meet opposite sides at D, E, and F. So this means that if

then AD, BE, and CF are concurrent (meaning the three lines meet at a single point, in this case it will be O).

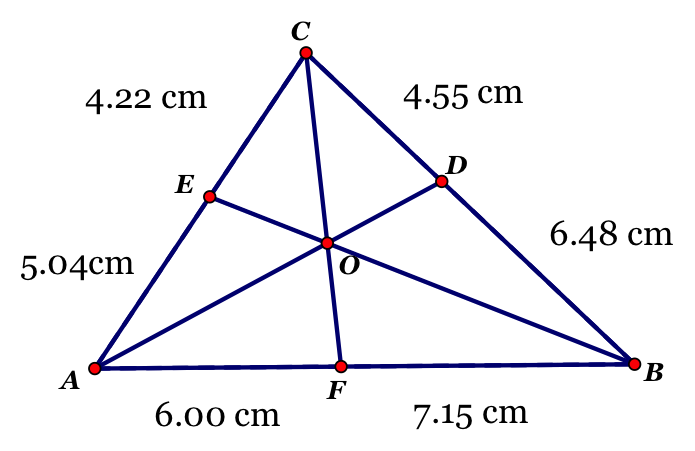
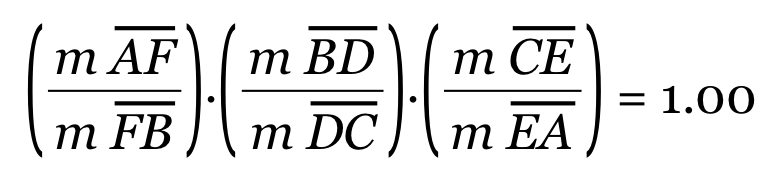
Note: AB is taken to be positive or negative depending on its position in relation to B. If A is to the left of B then AB has a positive length but if A is to the right of B then AB has a negative length. For example, AF/ FB is said to have positive value when F is between A and B and negative if it is not.

For the limited time we have for this class, we will focus on the positive length value of AB, since at this school level, it is closer to the types of problems we will be seeing. Just be aware that there is in fact a converse to this proof.

Directions: Match the letter of the definition with the number of each word (words and definitions will only be used once)
1. altitudes
2. incenter
3. orthocenter
4. medians
5. centroid
6. incircle
7. circumcenter
8. cevian

a. the intersection of the three perpendicular bisectors of a triangle
b. a line segment which joins a vertex of a triangle with a point on the opposite side (or its extension)
c. the intersection of the three angle bisectors of a triangle
d. cevians that are perpendicular to the legs opposite a given side of a triangle
e. the intersection of the three medians of a triangle
f. cevians from one of a triangle’s vertices to the midpoint of the opposite side
g. the intersection of the three altitudes of a triangle
h. a circle that is tangent to each of a polygon’s sides

III: Using GSP, create the 4 centers of a triangle. Email using the format LastF_Quiz1.doc. Be sure to label the, medians, altitudes, angle bisectors, incircle/ excircles when necessary.
1. centroid
2. circumcenter
3. orthocenter
4. incenter
5. EXTRA CREDIT: excenters

Goal: students should know all the points that make up the 9-point circle and be able to create the 9-point-circle on GSP
Lecture: how to create the 9-point circle (show a demonstration while students work along), note the points from the previous days that are included in the 9-point circle. Talk about relations between the 9-point circle and the circumcircle.

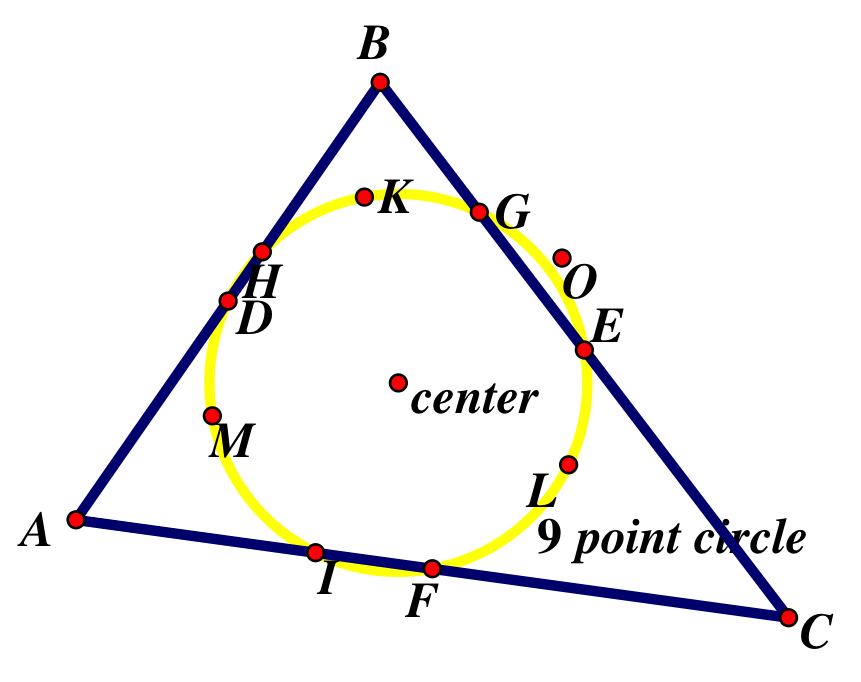
The points that create the 9-point circle are:
1. the midpoints of each side of the triangle (D,E, and F)
2. the foot of each altitude of the triangle (H, I, and G)
3. the midpoint of the line segment from each vertex of the triangle to the orthocenter (K, L, and M)

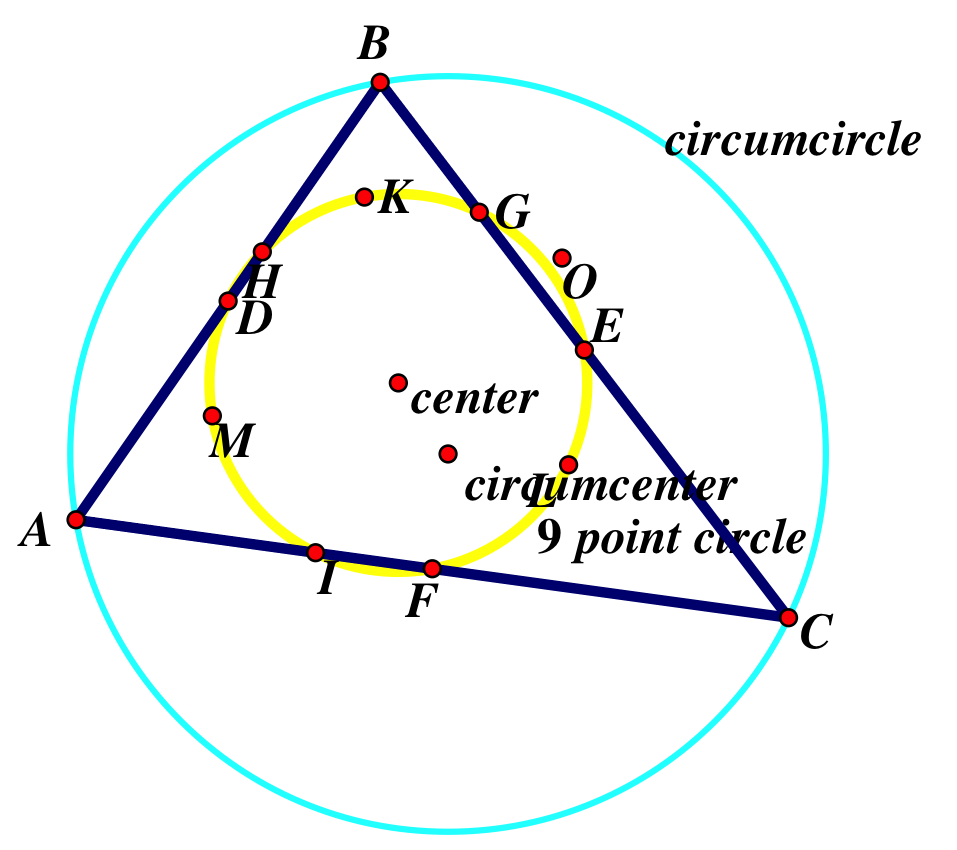
2. A 9-point circle bisects a line segment going from the corresponding triangle’s orthocenter to any point on its circumcircle

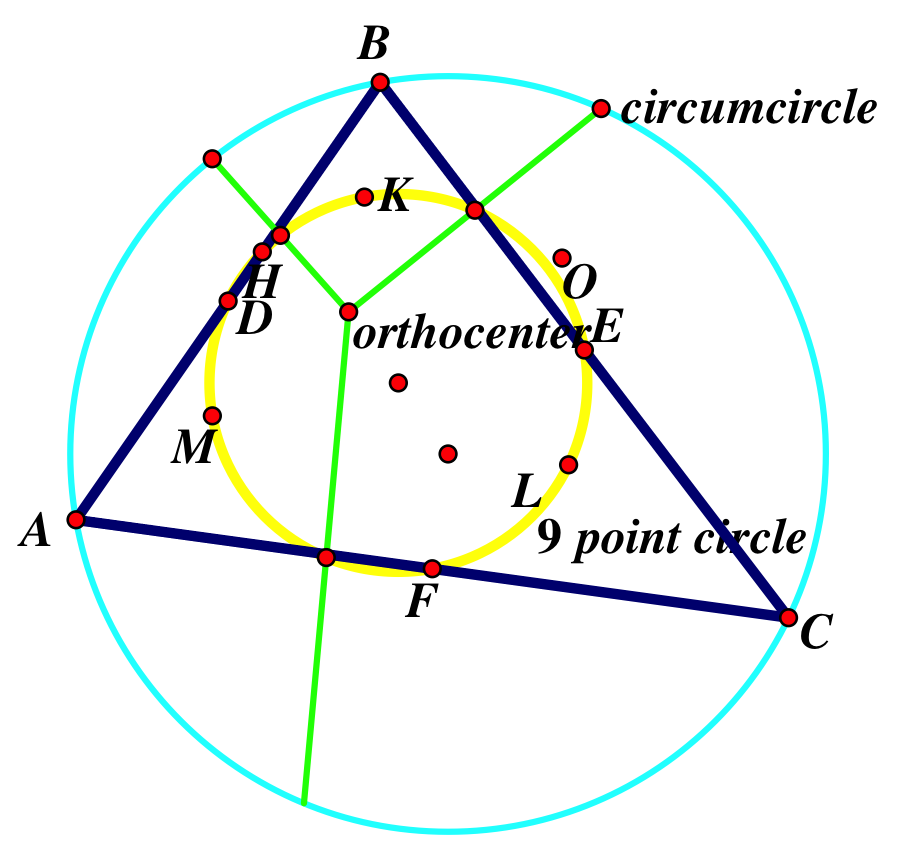
3. The center of any 9-point circle lies on that triangle’s Euler line (more about this on day 6)

4. The 9-point center lies at the centroid of four points that are made up by the triangle’s three vertices and its orthocenter

Goal: Students should understand what points make up the Euler Line
Lecture: Give demonstration on GSP while students work along as the same time, talk about relation to 9-point circle.
The Euler line (pronounced oiler) is a line determined only in triangles that are NOT equilateral. It passes through the orthocenter, circumcenter, centroid, and center of the 9-point circle.

1. orthocenter

2. center of 9-point circle

3. centroid

4. circumcenter

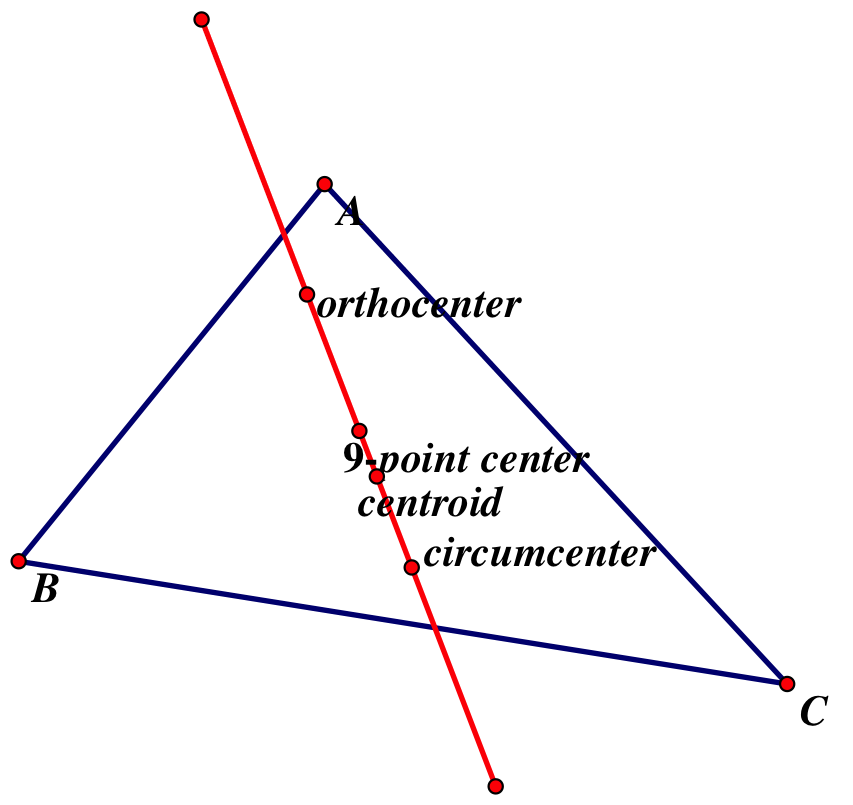
While these are the main 4 points of focus we will study on the Euler line, there are several other points worth noting as well:
-Exeter point
-de Longchamps point
-Schiffler point
-far-out point

Day 6: Quiz on 9-point circle and Euler line
I: Identify the points of the 9-point circle

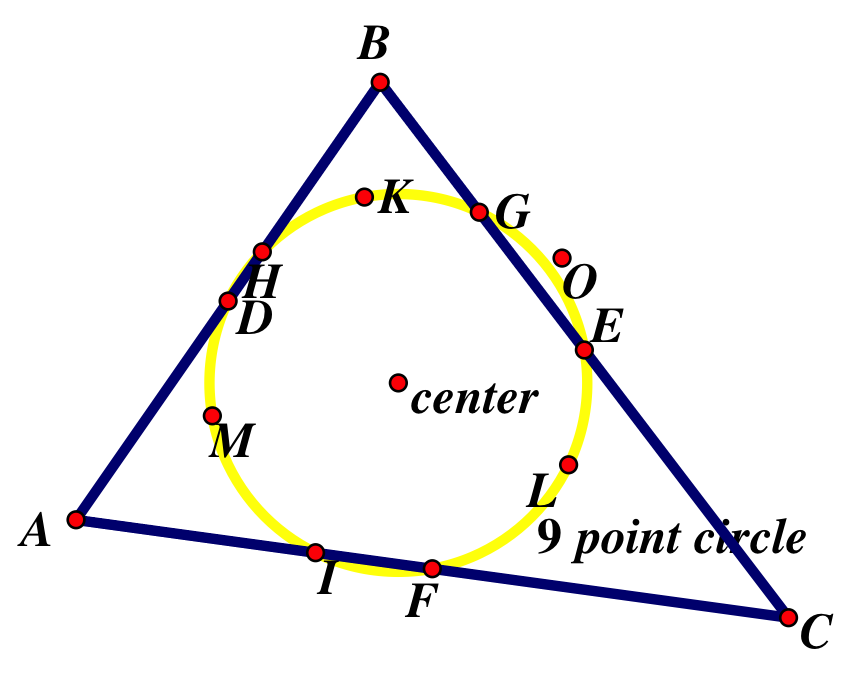
D: __________________________________
E: ___________________________________
F: ___________________________________
G: ___________________________________
H: ___________________________________
I: ____________________________________
K: ___________________________________
L: ___________________________________
M: ___________________________________

II: Fill in the blank

1. The radius of a triangle’s ________________ is ________________ the radius of that triangle’s 9-point circle.

2. The center of any 9-point circle lies on that triangle’s ____________________.

3. The 9-point center lies at the _________________ of four points that are made up by the triangle’s three ____________________ and its ____________________.

4. A 9-point circle _____________________ a line segment going from the corresponding triangle’s _____________________ to any point on its circumcircle.

5. The Euler line is determined from triangles that are ________________ ______________________.

IV: Short answer:

1. Name the points that make up the 9-point circle

2. Name the points that make up the Euler line

3. EXTRA CREDIT: Name the other 4 points that are also on the Euler line of a triangle (1 point each)

Day 7: Locus day 1

Goal: students should understand the basic definition of the locus of a triangle and be introduced to the main theorems involving the locus
Lecture: Explain and draw out for students the main theorems

Definition: set of points that satisfy a certain condition or rule.

While this is sort of abstract and difficult to grasp, here’s an example most people know but are not aware they know it.

A radius: set of points that are the same distance from the center of the circle

Angles in a circle

Proofs:

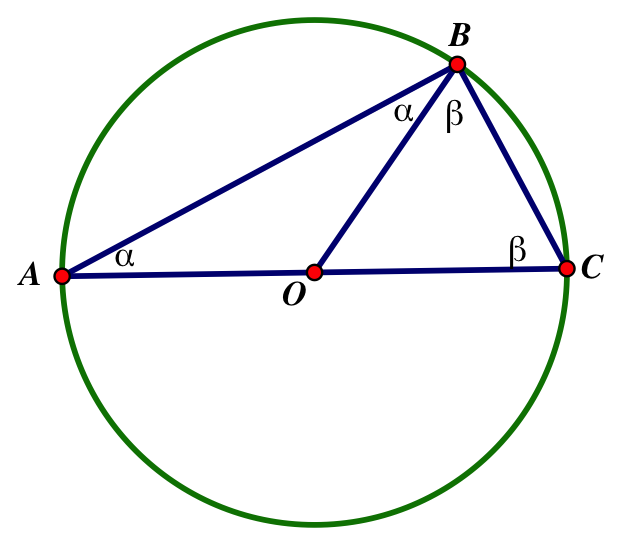
Invariance of angles in a circle (aka inscribed angles theorem):

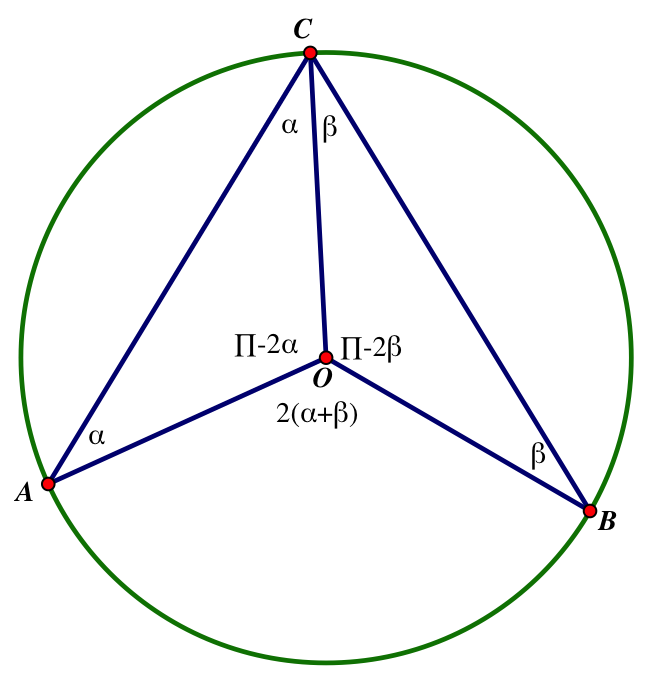
If A and B are two points on a circle, then for all points C on one of the arcs connecting them, the angle ACB is constant

Draw lines A, B, and C to the center of the circle O. Because all radii of a circle are equal then |OA|=|OB|=|OC|

|OA|=|OC| meaning AOC is isosceles and the angles a are equal because the angles opposite equal sides in an isosceles triangle are also equal.

Similarly, |OB|=|OC| therefore BOC is isosceles and the angles b are equal

Because the sum of the interior angles of a triangle are equal to 180 (denoted as π), it follows that angle AOC is equal to π -2a and the angle BOC is equal to π-2b

It follows that AOB equals 2(a+b) because the total angle around any point is 360 (or 2π).

Since angle AOB is constant then a+b is also constant and a+b is the angle ACB

Angles in a semicircle theorem (aka Thales’ Theorem):

This is commonly known as Thales’ Theorem. The diameter of a circle always subtends a right angle to any point on the circle.

Given: The interior angles of any triangle add up to 180 degrees

Proof:

Since OA=OB=OC, OBA and OBC are isosceles triangles therefore OBC=OCB and BAO=ABO

Let =BAO and =OBC

The three internal angles of ABC are ,, and .

Since the sum of the interior angles of a triangle add up to 180 we get

+()+=180

2+ 2= 180

2()=180

therefore, =90

Converse: the right triangle’s hypotenuse is the diameter of its circumcircle

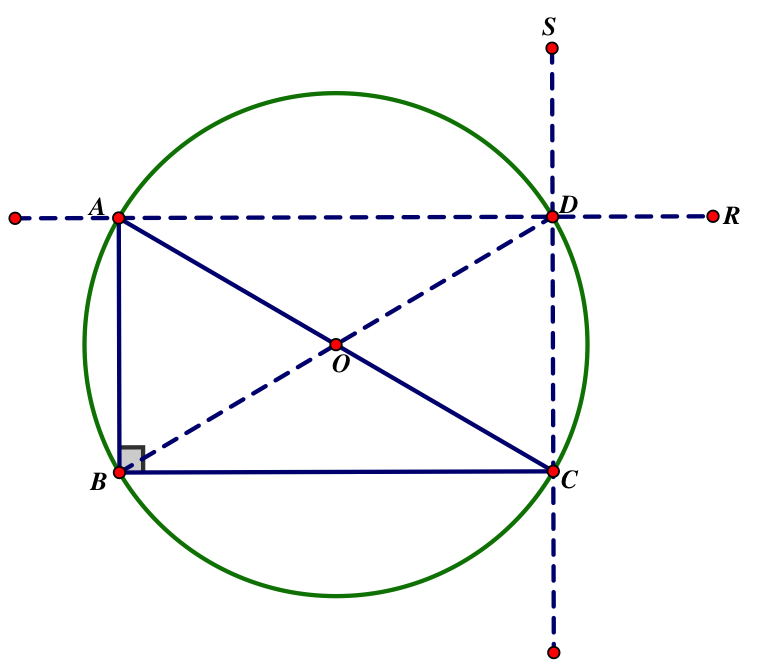
Given: adjacent angles in a parallelogram are supplementary, the diagonals of a rectangle are equal and cross each other in their mid-point

Proof:

Let there be a right angle ABC with a line R parallel to BC passing through A and a line S parallel to AB passing through C with a point of intersection at D

The quadrilateral ABCD forms a parallelogram by construction because the opposite sides are parallel. Since adjacent angles are supplementary and ABC is a right angle then angles BAD, BCD, and ADC are also right, meaning ABCD is a rectangle.

Let O be the point of intersection of the diagonals AC and BD. Then O is equidistant from A, B, and C. Therefore, O is the center of the circumcircle and the hypotenuse of ABC is the diameter of the circle.

Day 8: Locus day 2

Goal: Students should have a better grasp of the theorems

Lecture: refresh on theorems. Have students work in groups and go over theorems together and work on remembering the proofs and constructing the proofs

Day 9: Quiz on Locus points

State and prove the inscribed angles theorem:

State and prove Thales’ Theorem:

Day 10: Pythagorean relations day 1

Goal: for students to learn the individual proofs that go into making up Pythagorean’ Theorem

Lecture: theorems leading up to the Pythagorean theorem

Side Angle Side (SAS) axiom: If triangles ABC and A’B’C’ are such that

|AB|=|A’B’|, angle ABC=angle A’B’C’, |BC|=|B’C’|

then also,

|AC|=|A’C’|, angle BCA= angle B’C’A’, angle CAB= angle C’A’B’

basically, this just means that two triangles ABC and A’B’C’ are congruent if two sides and the included angle are equal

Angle Side Angle (ASA) axiom: two triangles ABC and A’B’C’ are congruent if two angles and the included side are equal

Side Side Side (SSS) axiom: two triangles ABC and A’B’C’ are congruent if all three sides are equal

Isosceles triangle theorem: If a triangle has two equal sides, then the angles opposite to these sides are also equal

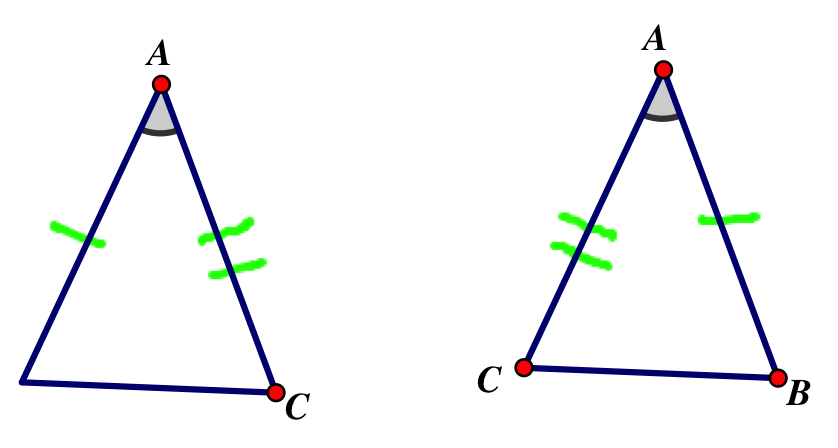
Proof:

Suppose that triangle ABC has |AB|=|AC|

Then triangles ABC and ACB, which are the same triangle, are congruent by SAS (their left and right sides are equal and angle A, which is the same in both triangles, is also equal)

Parallelogram side theorem: opposite sides of a parallelogram are equal

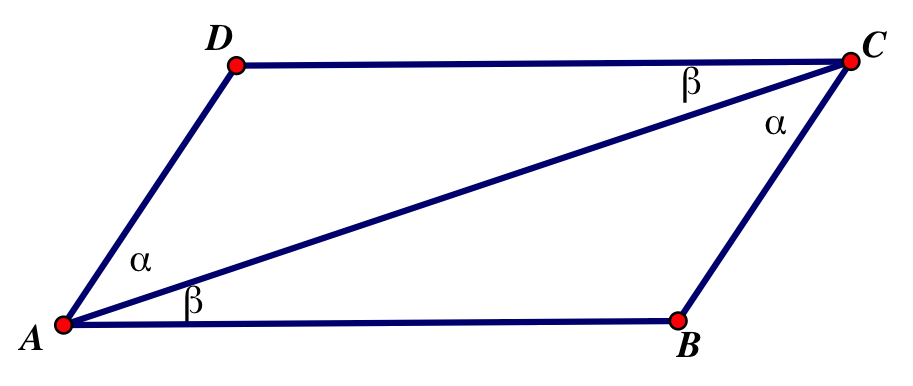
Divide the parallelogram into two triangles by a diagonal and prove these triangles are congruent

Proof:
They have a common side AC

Their corresponding angles a are equal, being alternate interior angles for the parallels AD and BC

Their corresponding b are equal, being alternate interior angles for the parallels AB and DC

Therefore, the triangles ABC and ADC are congruent by ASA. We also know that the opposite sides |AB|=|DC| and |AD|=|BC| because they are corresponding sides.

Day 11: Pythagorean relations day 2

Goal: for students to understand and learn Pythagorean’ theorem
Lecture: on Pythagorean theorem and its proof

Pythagorean theorem: for any right-angle triangle, the sum of the squares on the two shorter sides equal the square on the hypotenuse

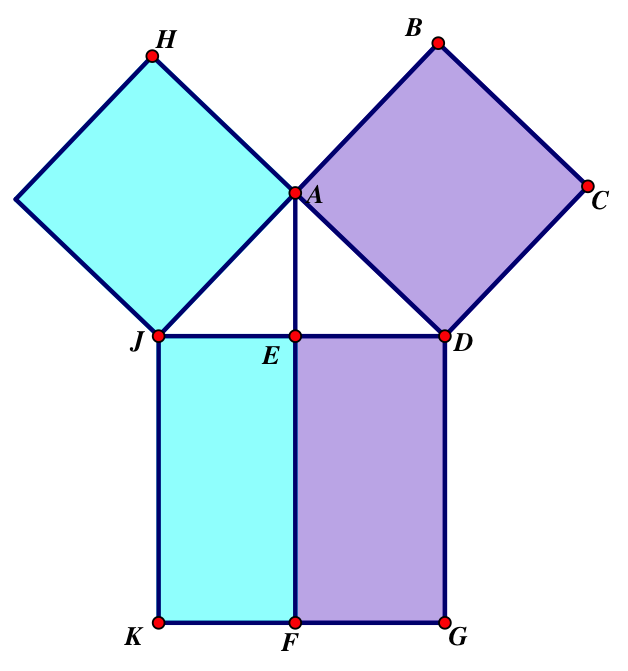
We want to prove that half of the purple square ABCD equals half of the purple square DEFG.

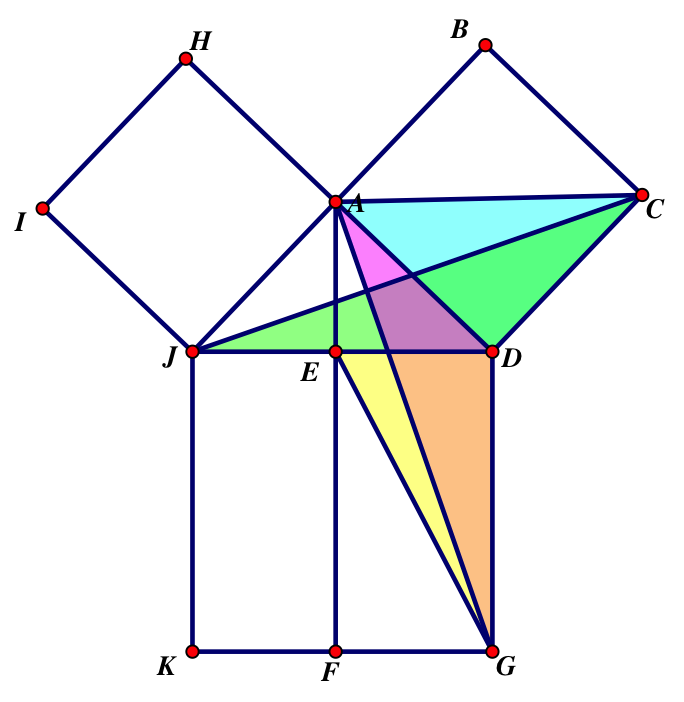
We will focus on 4 triangles ADC, ADG, JDC, and EDG.

ABCD, JDGK, and HIJA are squares

1. area of ADC=area JDC because they have the same base DC and their opposite corners A and J lie on a line parallel to DC (therefore, they have the same height)

2. area of JDC=area of ADG (congruent)

|DC|=|AD| because ABCD is a square

|JD|=|DG| because JDGK is a square

<JDC=<ADC+<ADJ=<ADJ+<JDG because <ADC and <JDG are right angles

Therefore, by SAS JDC is congruent to ADG

3. area of ADG=area of EDG because they have the same base DG and their opposite angles A and E lie on a line parallel to DG (therefore, they have the same height)

Day 12: Quiz on Pythagorean relations

State and prove the Pythagorean Theorem:

Return