

A Twist on Multiplication and Addition
Elizabeth Nelli
While addition is a topic area that elementary students learn, other cultures taught multiplication in a different method from our own. Here are some examples of different ways to add, that were most likely used before our country was even founded and before our own addition techniques were developed.
Pa-Kua
This is a type of addition used in China. The Liang I, or, “two principles” (the male yang ,—, and the female ying, - -) make up Pa-Kua. The — symbol means to add the number and the - - symbol means not to add the number. The order of the lines from top to bottom goes 1, 2, 4, 8, 16…and so on.
Beginning from right to left the following represents 0,1,2,3,4,5,6,7
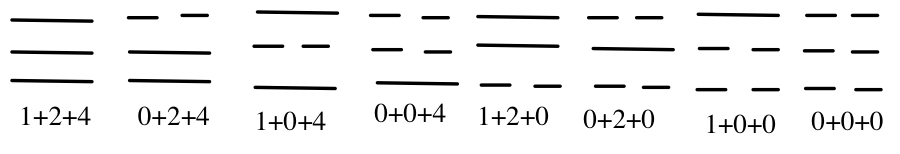
Here are some more complex numbers. Remember, whenever you see a - - symbol that means you skip that number, or basically it counts as 0.
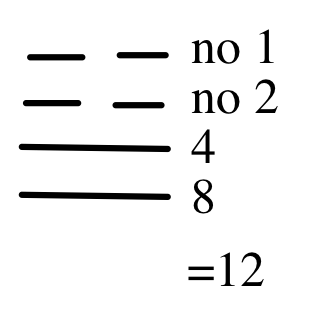
The Chinese also had to add numbers just as we do. Below is an example of addition using Pa-Kua.
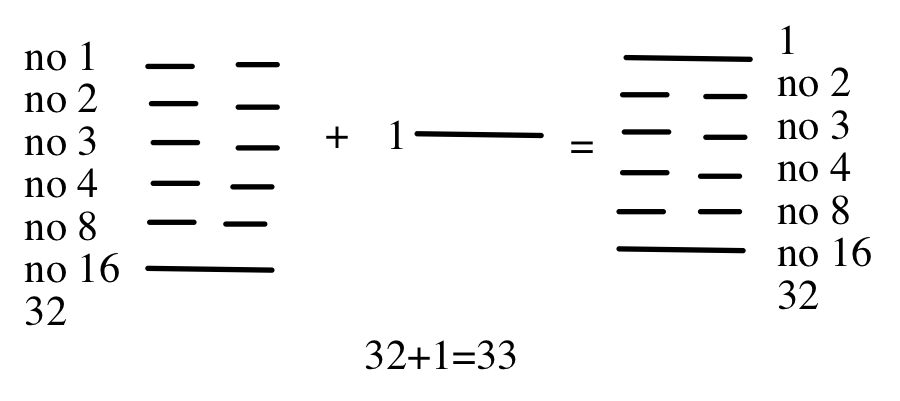
Hindu Add it on
The Hindus added from left to right as opposed to right to left like we are used to today.
Let's add 345 and 488

The numbers to be added are written one under the other as shown above.
3+4=7 and place the 7 above the hundreds place. Next, 4+8=12, which changes the 7 to an 8 (just like the carrying method we are used to) and puts a 2 over the tens place. Usually, the 7 would have been erased but to see the process, I have just crossed the 7 out and written the 8 above it. On to the units place; 5+8=13, which changes the 2 to a 3 and places a 3 above the units place. We now have our answer of 833.
Lilavati Addition
This process used the sum of the units, sum of the tens, the sum of the hundreds, and the sum of the sums in order to find the product of two numbers.
Again, we will use 345 and 488.

We have to line up all of the correct place values. The 3 of the 13 is placed farthest to the right. The 2 from the 12 goes lines up under the 1 from 13 from above, written into the tens place. The 7 lines up with the 1 from the above 12, moving into the hundreds place. Adding these all together from top to bottom gives the answer 833.
Now that we have talked about addition, let's move onto some multiplication. Learning multiplication is difficult for many students. Luckily, there are several ways to teach the topic. This can only be used for those students who are already familiar with basic addition and multiplication.
Here are three unorthodox types of multiplication.
Vedic Multiplication
write the problem down just as you would any other multiplication problem.
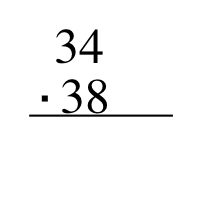
Multiply the units digits together

Cross multiply each other units digits with the tens digits. Add the products together (in this case we add 3x4=12 and 3x8=24 to get 36).

Multiply the tens digits together. Add the three rows to get the solution of 1292.

A second form of Vedic multiplication uses directed distance from 10.
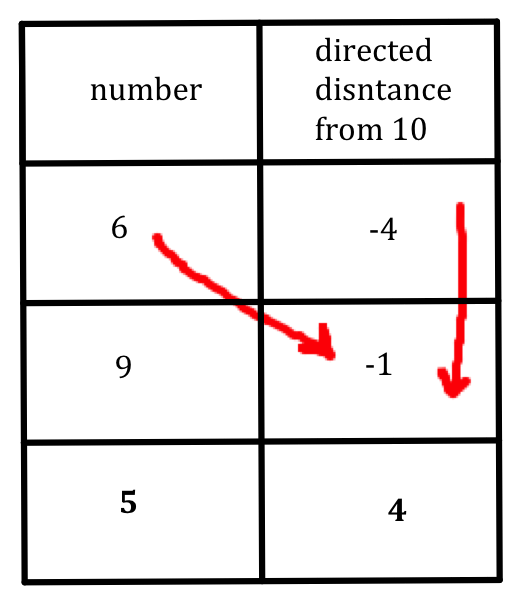
Say for example we are multiplying 6 and 9.
Write down their directed dissents from ten. Numbers smaller than 10 will have a negative value and numbers larger than 10 will have a positive value.

First multiply the numbers in the right hand column (-4x-1=4) and put this at the bottom of this column. Then find the sum of the crosswise numbers (6-1=5) and place this in the bottom of the left hand column. You can also use the sum of 9-4 which is also equal to 5. This is the answer to 6x9.
Let’s try an example when we have to carry. We'll do 7x6.
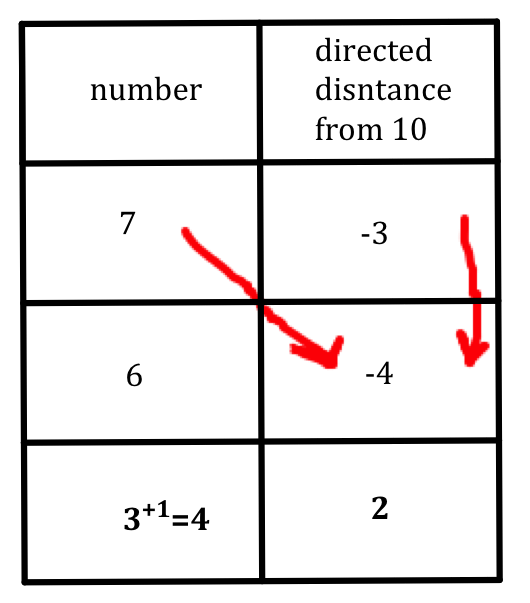
Since -3x(-4)=12, we have to carry a one over to the bottom left hand column. 7-4=3, but we add the 1 from the 12 to get 4. This gives us the answer of 7x6=42.
Numbers larger than 10 work as well with this method. The directed distance from 10 is now positive as opposed to negative with the numbers smaller than 10.

By carrying the 1 over from 5x2=10, we get 17+1 in the bottom left hand column to give us the answer of 15x12=180.
To reiterate what was said in the beginning, you can now see why it is important that a basic knowledge of addition and multiplication is still needed to perform this type of multiplication. The same applies for the other methods as well.
Japanese Stick Multiplication
The Japanese use a unique form of multiplication that involves the crisscrossing of sticks and counting the intersections to get the product of two numbers.
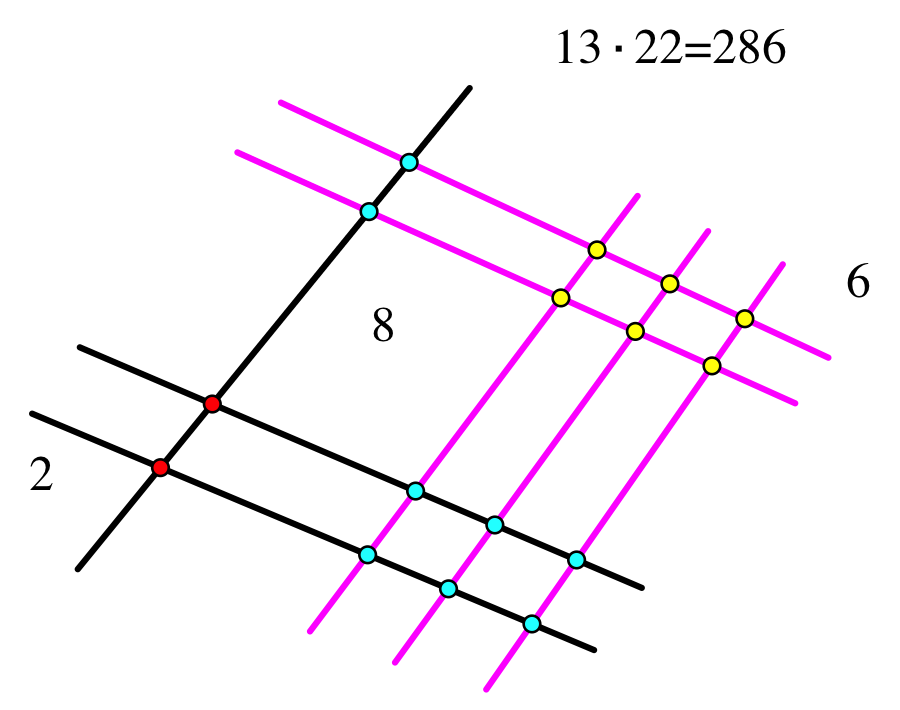
The crossing of the purple lines (the 3 and the 2) which are the ones digit of both numbers gives 6 intersections. The crossing of the purple and black lines (the 3 and 2 and the 1 and 2) which is the tens digit of the 13 and the ones digit of the 22 gives 8 intersections. The crossing of the black lines (the 1 and 2) which are the tens digit of both numbers gives 2 intersections. The units digits of the solution are the intersections in yellow, the tens digits are the intersections in blue, and the hundreds digits are the intersections in red. This gives the answer of 286.
Arabic Multiplication
This next form of multiplication is attributed to the Arabians. It involves a lattice diagram and the additions are performed diagonally.
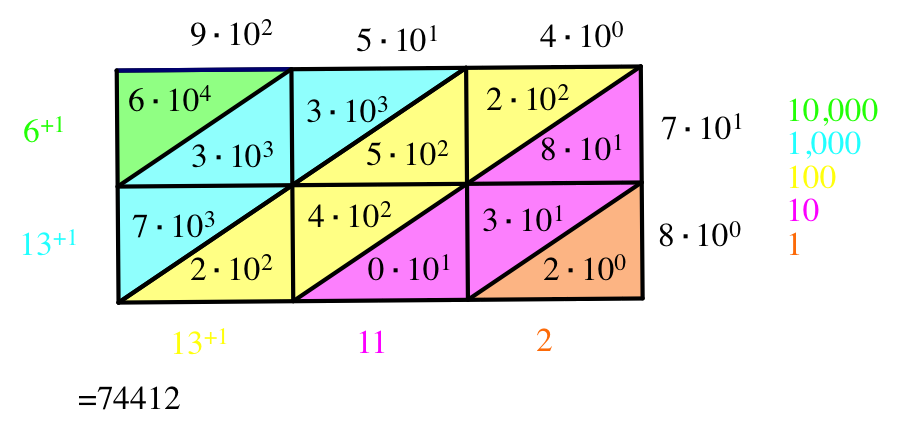
To fill in the boxes, we multiply as though we are using a regular graph: 7x4=28, 8x4=32, 7x5=35, 8x5=40, 7x9=63, 8x9=72. Split the tens digit and ones digit into the 2 separate diagonals of the boxes. The bottom right diagonal is the units place, and each diagonal after that follows in order of tens, hundreds, thousands, and ten thousands. We now add all the diagonals together to get the product of 954 and 78. We have to carry using this method. 2 is the units number because we do not have to add any other number in the units diagonal. 8+3+0=11. 2+5+4+2=13, but we have to add the 1 from the 11 in the tens place so we get 14. 3+3+7=13 but again we have to add the 1 from the hundredths place so we get 14. 6 is in the ten thousandths place, but we need to add the 1 from the thousandths place to get 7. So the answer to 954x78=74412.